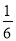题目内容
写出下列事件发生的可能性,并标在图中的大致位置上.
(1)袋中有10个红球,摸到红球;
(2)袋中有10个红球,摸到白球;
(3)一副混合均匀的扑克牌(除去大、小王),从中任意抽取一张,这一张恰好是A;
(4)一个布袋中有2个黑球和2个白球,从中任意摸出一个球,恰好是黑球;
(5)任意掷出一个质地均匀的骰子(每个面上分别标有数字1,2,3,4,5,6),朝上一面的数字大于2.
(1)1(2)0(3) (4) (5) 【解析】试题分析:根据题意,分别找出事件发生的所有可能,然后找出符合条件的可能,然后求出概率即可,最后根据事件发生的可能性大小,把它们标注在数轴上. 试题解析:(1)P==1. (2)P==0. (3)P==. (4)P==. (5)P==.标注如图所示.
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:
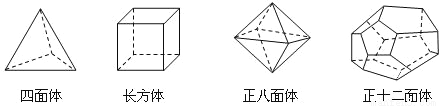
(1)根据上面多面体的模型,完成表格中的空格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 12 | |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?
6;6;6 【解析】试题分析: (1)由图形可得; (2)观察可得顶点数+面数-棱数=2; (3)代入(2)中的式子即可得到面数; 试题解析: (1)6;6;6 (2)四面体的棱数为6;正八面体的顶点数为6;关系式为:V+F﹣E=2; (3)由题意得:F﹣8+F﹣30=2, 解得F=20.

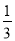 B.
B. 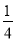 C.
C. 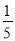 D.
D.