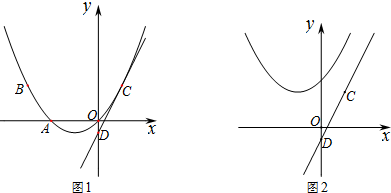题目内容
14.随着机构改革工作的深入进行,各单位要减员增效.有一家公司现有职员160人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利0.1万元,但公司需支付下岗职员每人每年4万元的生活费,并且该公司正常运转所需人数不得小于现有员工的$\frac{3}{4}$,设裁员x人,可获得的经济效益为y万元.(1)求y与x的函数关系式;
(2)为获得最大的经济效益,该公司应裁员多少人?
分析 (1)设裁员x人,可获得的经济效益为y=留岗职员数×每个留岗职员创利-下岗职员数×每个下岗职员生活费.
(2)配方后利用二次函数性质可求出结论.
解答 解:(1)设裁员x人,可获得的经济效益为y万元.则
y=(160-x)(10+0.1x)-4x=-$\frac{1}{10}$x2+2x+1600;
(2)y=-$\frac{1}{10}$x2+2x+1600=-$\frac{1}{10}$(x-10)2+1610,
∵公司正常运转所需人数不得小于现有员工的$\frac{3}{4}$,
∴160-x≥$\frac{3}{4}$×160,
∴0<x≤40,
∴当x=10时,获得的经济效益最大,最大经济效益是1610元.
故为获得最大的经济效益,该公司应裁员10人.
点评 本题主要考查了二次函数的实际应用,解决此类问题的关键是建立数学模型,联系二次函数的性质和图象,解决最值问题.

练习册系列答案
相关题目
 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.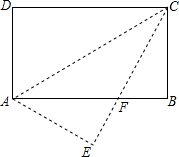 如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,点D落在点E处,CE与AB交于点F.
如图,在矩形ABCD中,AB=16,BC=8,将矩形沿AC折叠,点D落在点E处,CE与AB交于点F.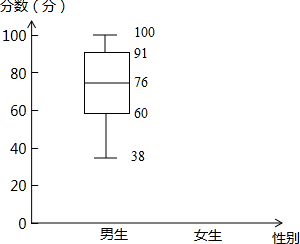 在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;
在统计数据时,我们将所有数值由小到大排列并分成四等份,每一部分大约包含25%的数据项,处于三个分割点位置的数从小到大分别记为Q1、Q2、Q3.再将最小值记为M,最大值记为N;