题目内容
16. 如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为(-2,0).
如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为(-2,0).
分析 由矩形OABC中,点B的坐标为(2,4),可求得点C的坐标,又由矩形OABC与矩形ODEF是位似图形,P是位似中心,点C的对应点点E的坐标为(-1,2),即可求得其位似比,继而求得答案.
解答 解:∵四边形OABC是矩形,点B的坐标为(2,4),
∴OC=AB=4,OA=2,
∴点C的坐标为:(0,4),
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点E的坐标为(-1,2),
∴位似比为1:2,
∴OP:AP=OD:AB=1:2,
设OP=x,则$\frac{x}{x+2}=\frac{1}{2}$,
解得:x=2,
∴OP=2,
即点P的坐标为:(-2,0).
故答案为:(-2,0).
点评 此题考查了位似变换的性质.注意求得矩形OABC与矩形ODEF的位似比是解此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
8.在Rt△ABC中,sinA=$\frac{1}{2}$,则tanA的值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{1}{2}$ |

 与三角形的一边和其他两边的延长线都相切的圆叫做这个三角形的旁切圆,其圆心叫做这个三角形的旁心.如图,△ABC的三个顶点的坐标分别为A(-3,0),B(3,0),C(0,4).则△ABC位于第二象限的旁心D的坐标是(-5,4).
与三角形的一边和其他两边的延长线都相切的圆叫做这个三角形的旁切圆,其圆心叫做这个三角形的旁心.如图,△ABC的三个顶点的坐标分别为A(-3,0),B(3,0),C(0,4).则△ABC位于第二象限的旁心D的坐标是(-5,4).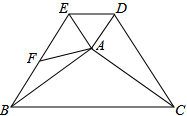 如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.