题目内容
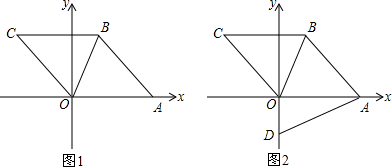
平面直角坐标系中,四边形ABCO是菱形,点C的坐标为(-3,4),点A在x轴的正半轴上,O为坐标原点,连接OB,抛物线y=ax2+bx+c经过C、O、A三点.
(1)直接写出这条抛物线的解析式;
(2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCO的面积为S2,当S1≤
S2时,求点E的纵坐标n的取值范围;
(3)如图2,D(0,-
)为y轴上一点,连接AD,动点P从点O出发,以
个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O-A-B方向运动,设点P运动时间为t秒(0<t≤6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.
(1)直接写出这条抛物线的解析式;
(2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCO的面积为S2,当S1≤
| 1 |
| 4 |
(3)如图2,D(0,-
| 5 |
| 2 |
| ||
| 5 |

考点:二次函数综合题,三角形的面积
专题:压轴题,动点型
分析:(1)求得菱形的边长,则A的坐标可以求得,然后利用待定系数法即可求得函数的解析式;
(2)首先求得菱形的面积,即可求得S1的范围,当S1取得最大值时即可求得直线的解析式,则n的值的范围即可求得;
(3)分当1<t<3.5时和3.5≤t≤6时两种情况进行讨论,依据相似三角形的对应边的比相等,即可列方程求解.
(2)首先求得菱形的面积,即可求得S1的范围,当S1取得最大值时即可求得直线的解析式,则n的值的范围即可求得;
(3)分当1<t<3.5时和3.5≤t≤6时两种情况进行讨论,依据相似三角形的对应边的比相等,即可列方程求解.
解答:解:(1)∵C点坐标为(-3,4),四边形ABCD是菱形,
∴OA=OC=5,A点坐标为(5,0),
根据题意得:
,
解得:
,
则抛物线的解析式是:y=
x2-
x;
(2)设BC与y轴相交于点G,则S2=OG•BC=20,
∴S1≤5,
又OB所在直线的解析式是y=2x,OB=
=2
,
∴当S1=5时,△EBO的OB边上的高是
.
如图1,设平行于OB的直线为y=2x+b,则它与y轴的交点为M(0,b),与抛物线对称轴x=
交于点E(
,n).
过点O作ON⊥ME,点N为垂足,若ON=
,由△MNO∽△OGB,得OM=5,
∴y=2x-5,
由
,
解得:y=0,
即E的坐标是(
,0).
∵与OB平行且到OB的距离是
的直线有两条.
∴由对称性可得另一条直线的解析式是:y=2x+5.
则E′的坐标是(
,10).
由题意得得,n的取值范围是:0≤n≤10且n≠5.
(3)如图2,动点P、Q按题意运动时,
当1<t<3.5时,
OP=
t,BP=2
-
t,OQ=2(t-1),
连接QP,当QP⊥OP时,有
=sin∠BOQ=sin∠OBC=
,
∴PQ=
(t-1),
若
=
,则有
=
,
又∵∠QPB=∠DOA=90°,
∴△BPQ∽△AOD,
此时,PB=2PQ,即2
-
t=
(t-1),
10-t=8(t-1),
∴t=2;
当3.5≤t≤6时,QB=10-2(t-1)=12-2t,连接QP.
若QP⊥BP,
则有∠PBQ=∠ODA,
又∵∠QPB=∠AOD=90°,
∴△BPQ∽△DOA,
此时,QB=
PB,即12-2t=
(2
-
t),12-2t=10-t,
∴t=2(不合题意,舍去).
若QP⊥BQ,则△BPQ∽△DAO,
此时,PB=
BQ,
即2
-
t=
(12-2t),2-
t=12-2t,
解得:t=
.
则t的值为2或
.
∴OA=OC=5,A点坐标为(5,0),
根据题意得:
|
解得:
|
则抛物线的解析式是:y=
| 1 |
| 6 |
| 5 |
| 6 |
(2)设BC与y轴相交于点G,则S2=OG•BC=20,
∴S1≤5,
又OB所在直线的解析式是y=2x,OB=
| OG2+GB2 |
| 5 |
∴当S1=5时,△EBO的OB边上的高是
| 5 |
如图1,设平行于OB的直线为y=2x+b,则它与y轴的交点为M(0,b),与抛物线对称轴x=
| 5 |
| 2 |
| 5 |
| 2 |
过点O作ON⊥ME,点N为垂足,若ON=
| 5 |
∴y=2x-5,
由
|
解得:y=0,
即E的坐标是(
| 5 |
| 2 |
∵与OB平行且到OB的距离是
| 5 |
∴由对称性可得另一条直线的解析式是:y=2x+5.
则E′的坐标是(
| 5 |
| 2 |
由题意得得,n的取值范围是:0≤n≤10且n≠5.

(3)如图2,动点P、Q按题意运动时,
当1<t<3.5时,
OP=
| ||
| 5 |
| 5 |
| ||
| 5 |
连接QP,当QP⊥OP时,有
| PQ |
| OQ |
| 2 | ||
|
∴PQ=
| 4 | ||
|
若
| PQ |
| PB |
| 1 |
| 2 |
| PQ |
| PB |
| OD |
| OA |
又∵∠QPB=∠DOA=90°,
∴△BPQ∽△AOD,
此时,PB=2PQ,即2
| 5 |
| ||
| 5 |
| 8 | ||
|
10-t=8(t-1),
∴t=2;
当3.5≤t≤6时,QB=10-2(t-1)=12-2t,连接QP.
若QP⊥BP,
则有∠PBQ=∠ODA,
又∵∠QPB=∠AOD=90°,
∴△BPQ∽△DOA,
此时,QB=
| 5 |
| 5 |
| 5 |
| ||
| 5 |
∴t=2(不合题意,舍去).
若QP⊥BQ,则△BPQ∽△DAO,
此时,PB=
| 5 |
即2
| 5 |
| ||
| 5 |
| 5 |
| 1 |
| 5 |
解得:t=
| 50 |
| 9 |
则t的值为2或
| 50 |
| 9 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
 画出如图所示的由5个小立方块组成的几何体的三个视图.
画出如图所示的由5个小立方块组成的几何体的三个视图.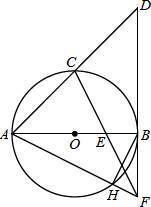 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是
 如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.