题目内容
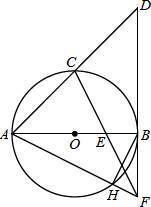 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是 |
| AB |
(1)求证:AC=CD;
(2)若OB=2,求BH的长.
考点:切线的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)连接OC,由C是
的中点,AB是⊙O的直径,则CO⊥AB,再由BD是⊙O的切线,得BD⊥AB,从而得出OC∥BD,即可证明AC=CD;
(2)根据点E是OB的中点,得OE=BE,可证明△COE≌△FBE(ASA),则BF=CO,即可得出BF=2,由勾股定理得出AF=
,由AB是直径,得BH⊥AF,可证明△ABF∽△BHF,即可得出BH的长.
 |
| AB |
(2)根据点E是OB的中点,得OE=BE,可证明△COE≌△FBE(ASA),则BF=CO,即可得出BF=2,由勾股定理得出AF=
| AB2+BF2 |
解答: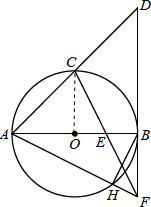 (1)证明:连接OC,
(1)证明:连接OC,
∵C是
的中点,AB是⊙O的直径,
∴CO⊥AB,
∵BD是⊙O的切线,
∴BD⊥AB,
∴OC∥BD,
∵OA=OB,
∴AC=CD;
(2)解:∵E是OB的中点,
∴OE=BE,
在△COE和△FBE中,
,
∴△COE≌△FBE(ASA),
∴BF=CO,
∵OB=2,
∴BF=2,
∴AF=
=2
,
∵AB是直径,
∴BH⊥AF,
∴△ABF∽△BHF,
∴
=
,
∴AB•BF=AF•BH,
∴BH=
=
=
.
 (1)证明:连接OC,
(1)证明:连接OC,∵C是
 |
| AB |
∴CO⊥AB,
∵BD是⊙O的切线,
∴BD⊥AB,
∴OC∥BD,
∵OA=OB,
∴AC=CD;
(2)解:∵E是OB的中点,
∴OE=BE,
在△COE和△FBE中,
|
∴△COE≌△FBE(ASA),
∴BF=CO,
∵OB=2,
∴BF=2,
∴AF=
| AB2+BF2 |
| 5 |
∵AB是直径,
∴BH⊥AF,
∴△ABF∽△BHF,
∴
| AB |
| BH |
| AF |
| BF |
∴AB•BF=AF•BH,
∴BH=
| AB•BF |
| AF |
| 4×2 | ||
2
|
4
| ||
| 5 |
点评:本题考查了切线的性质以及全等三角形的判定和性质、勾股定理,是中档题,难度不大.

练习册系列答案
相关题目
下列说法正确的是( )
| A、0的平方根是0 | ||||
| B、9的立方根是3 | ||||
C、
| ||||
D、
|
 =0,
=0, =-5,
=-5, =12,
=12, =
=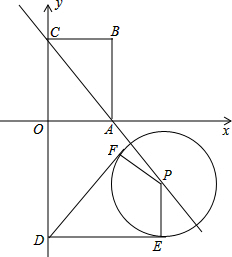 已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,-5),点P是直线AC上的一动点.
已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A(3,0)、B(3,4)、C(0,4).点D在y轴上,且点D的坐标为(0,-5),点P是直线AC上的一动点.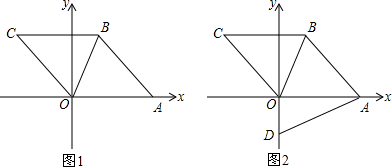
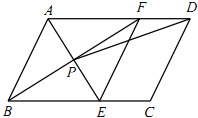 如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.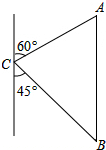 如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据:
如图,有小岛A和小岛B,轮船以45km/h的速度由C向东航行,在C处测得A的方位角为北偏东60°,测得B的方位角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结果保留整数,参考数据: