题目内容
17.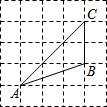 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
分析 首先构造以A为锐角的直角三角形,然后利用正切的定义即可求解.
解答  解:连接BD.
解:连接BD.
则BD=$\sqrt{2}$,AD=2$\sqrt{2}$,
则tanA=$\frac{BD}{AD}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$.
故答案是D.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,构造直角三角形是本题的关键.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (ab)2=ab2 | C. | a•a2=a3 | D. | (a3)2=a5 |
9. 如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
 如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )
如图,AB∥DE,AC⊥CD,并且∠A=35°,则∠D的度数为( )| A. | 55° | B. | 45° | C. | 30° | D. | 60° |
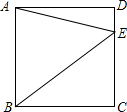 如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为8,DE=1,则线段BE=5.
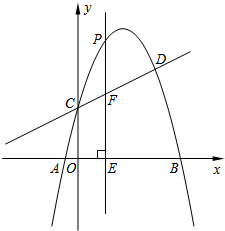 如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点C在y轴上,点D的横坐标为3,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=-x2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点C在y轴上,点D的横坐标为3,点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.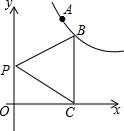 已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点
已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点 一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最少可以由10个这样的正方体组成.
一个由若干个相同的正方体组成的几何体,其主视图和左视图如图所示,这个几何体最少可以由10个这样的正方体组成.