题目内容
 如图,点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2,AB=AD,请添加一个条件,使△ABC≌△ADE,则需添加的条件是________.
如图,点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2,AB=AD,请添加一个条件,使△ABC≌△ADE,则需添加的条件是________.
∠ADB=∠AED或BD=DE或∠1=∠DAE
分析:由∠1=∠2,可证∠ABD=∠ADE,然后结合已知条件,根据全等三角形判定定理AAS,SAS,ASA即可得出证明△ABC≌△ADE的条件.此题开放性较强,答案不唯一.
解答:证明:∠ADC=∠2+∠ADE=∠ABD+∠1
∴∠ABD=∠ADE,
又∵AB=AD,
∴如∠ADB=∠AED,
则△ABC≌△ADE(AAS)
故答案为:∠ADB=∠AED或BD=DE或∠1=∠DAE.
点评:此题主要考查学生对全等三角形的判定和三角形内角和定理的理解和掌握.解答此题的关键是根据内角和定理求证∠ABD=∠ADE.
分析:由∠1=∠2,可证∠ABD=∠ADE,然后结合已知条件,根据全等三角形判定定理AAS,SAS,ASA即可得出证明△ABC≌△ADE的条件.此题开放性较强,答案不唯一.
解答:证明:∠ADC=∠2+∠ADE=∠ABD+∠1
∴∠ABD=∠ADE,
又∵AB=AD,
∴如∠ADB=∠AED,
则△ABC≌△ADE(AAS)
故答案为:∠ADB=∠AED或BD=DE或∠1=∠DAE.
点评:此题主要考查学生对全等三角形的判定和三角形内角和定理的理解和掌握.解答此题的关键是根据内角和定理求证∠ABD=∠ADE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 25、如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.
25、如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.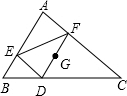 AC于点F.又知BC=5.
AC于点F.又知BC=5. 10、已知:如图,点D在△ABC的边BC上,DE∥AC交AB于E,DF∥AB交AC于F.
10、已知:如图,点D在△ABC的边BC上,DE∥AC交AB于E,DF∥AB交AC于F.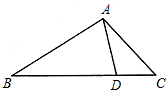 如图,点D在△ABC边BC上,且∠ADC=∠BAC,若AC=x,CD=x-2,BD=2x-2,则x的值是
如图,点D在△ABC边BC上,且∠ADC=∠BAC,若AC=x,CD=x-2,BD=2x-2,则x的值是 如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.