题目内容
11.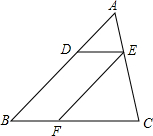 如图,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=$\frac{1}{2}$BD,则$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=( )
如图,点D、E、F分别在△ABC的边AB、AC、BC上,且DE∥BC,EF∥AB,若AD=$\frac{1}{2}$BD,则$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 根据已知条件得到$\frac{AD}{AB}$=$\frac{1}{3}$,$\frac{BD}{AB}$=$\frac{2}{3}$,根据平行四边形的性质得到EF=BD,根据相似三角形的性质即可得到结论.
解答 解:∵AD=$\frac{1}{2}$BD,
∴$\frac{AD}{AB}$=$\frac{1}{3}$,$\frac{BD}{AB}$=$\frac{2}{3}$,
∵DE∥BC,EF∥AB,
∴四边形DBFE是平行四边形,
∴EF=BD,
∴$\frac{EF}{AB}$=$\frac{2}{3}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=$\frac{1}{9}$,
∴S△ADE=$\frac{1}{9}$S△ABC,
∵EF∥AB,
∴△CEF∽△CAB,
∴$\frac{{S}_{△CEF}}{{S}_{△CAB}}$=($\frac{EF}{AB}$)2=$\frac{4}{9}$,
∴S△CEF=$\frac{4}{9}$S△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=$\frac{1}{4}$,
故选A.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,将三角板的直角顶点放在直尺的一边上,若∠1=60°,则∠2的度数为30°.
如图,将三角板的直角顶点放在直尺的一边上,若∠1=60°,则∠2的度数为30°.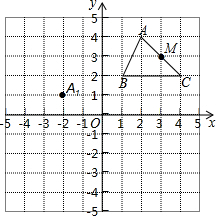 如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点.
如图,在平面直角坐标系中,是边长为1的正方形网格,△ABC的顶点均在图中网格的格点上,M为AC中点. 如图,在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=7,则点D到斜边AB的距离为7.
如图,在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=7,则点D到斜边AB的距离为7.