题目内容
17．
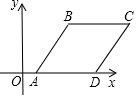如图，在平面直角坐标系中，菱形ABCD的边AD在x轴的正半轴上，若点A，B的坐标分别为（1，0）、（4，4），则点C的坐标为（6，0）．
分析 作辅助线，构建直角三角形，根据点B和A的坐标表示AE、BE的长，利用勾股定理求AB的长，则边长AD=5，写出D的坐标．
解答 
解：过B作BE⊥x轴于E，
∵B（4，4），
∴OE=BE=4，
∵A（1，0），
∴OA=1，
∴AE=3，
在Rt△AEB中，AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵四边形ABCD是菱形，
∴AC=AB=5，
∴OC=5+1=6，
∴C（6，0），
故答案为：（6，0）．
点评 本题考查了菱形的性质、坐标与图形物点，菱形具有平行四边形的一切性质；菱形的四条边都相等；属于基础题．
练习册系列答案
相关题目
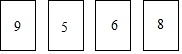康康家购置了一辆新车，爸爸妈妈商议确定车牌号，前四位选定为鲁DF32后，对后两位数字意见有分歧，最后决定由毫不知情的康康从如图排列的四个数字中随机划去两个，剩下的两个数字从左到右组成两位数，续在DF32之后，则选中的车牌号为DF3258的概率是$\frac{1}{6}$．
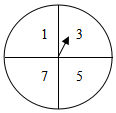A超市在一次周年庆典当天开展购物抽奖活动，凡当天在该超市购物的顾客，均有一次抽奖机会，抽奖规则如下：将如图所示的图形转盘平均分成四个扇形，分别标上1，3，5，7四个数字，抽奖者连续转动转盘两次，当每次停止后指针所指扇形内的数为每次所得数（若指针指在分界处重转），当两次所得数字之和为2时，返现金20元，当两次所得数字之和为4时，返现金10元，当两次所得数字之和为6时，返现金5元．
在平面直角坐标系中，已知A（0，4）、B（1，0）、C（4，0），D为线段BC上的动点，以AD为边向右侧作正方形ADEF，连CF交DE于P，则CP的最大值为1．
如图所示，将△ABC绕其顶点A顺时针旋转20°后得△ADE，则∠BAD的度数为20°．