题目内容
如图,在半径为 ,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在
,圆心角等于45°的扇形AOB内部作一个正方形CDEF,使点C在OA上,点D、E在OB上,点F在 上,则阴影部分的面积为(结果保留π) .
上,则阴影部分的面积为(结果保留π) .
【答案】分析:首先要明确S阴影=S扇形OAB-S△OCD-S正方形CDEF,然后依面积公式计算即可.
解答: 解:连接OF,
解:连接OF,
∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
于是Rt△OFE中,OE=2EF,
∵OF= ,EF2+OE2=OF2,
,EF2+OE2=OF2,
∴EF2+(2EF)2=5,
解得:EF=1,
∴EF=OD=CD=1,
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF= -
- ×1×1-1×1=
×1×1-1×1= .
.
点评:本题失分率较高,学生的主要失误在于找不到解题的切入点,不知道如何添加辅助线,也有学生对直角三角形三边关系不熟悉,误认为∠FOB=30°造成失误.
解答:
 解:连接OF,
解:连接OF,∵∠AOD=45°,四边形CDEF是正方形,
∴OD=CD=DE=EF,
于是Rt△OFE中,OE=2EF,
∵OF=
 ,EF2+OE2=OF2,
,EF2+OE2=OF2,∴EF2+(2EF)2=5,
解得:EF=1,
∴EF=OD=CD=1,
∴S阴影=S扇形OAB-S△OCD-S正方形CDEF=
 -
- ×1×1-1×1=
×1×1-1×1= .
.点评:本题失分率较高,学生的主要失误在于找不到解题的切入点,不知道如何添加辅助线,也有学生对直角三角形三边关系不熟悉,误认为∠FOB=30°造成失误.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
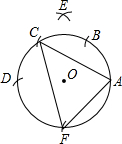 如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )
如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心A到C的距离为半径画弧,两弧交于E,以A为圆心O到E的距离为半径画弧,交⊙O于F.则△ACF面积是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在半径为5的⊙O中,弦AB=8,圆心O到弦AB的距离等于( )
如图,在半径为5的⊙O中,弦AB=8,圆心O到弦AB的距离等于( )| A、5 | B、4 | C、3 | D、6 |
 如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是( )
如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是( ) 如图,在半径为5的⊙O中,点A、B在⊙O中,∠AOB=90°,点C是
如图,在半径为5的⊙O中,点A、B在⊙O中,∠AOB=90°,点C是
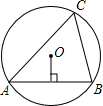 如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=
如图,在半径为2的⊙O中,圆心0到弦AB的距离为1,C为AB上方圆弧上任意一点,则∠ACB=