题目内容
如果有理数a,b满足|a-2|+(1-b)2=0,
(1)试求:
+
+
+…+
的值
(2)试求:a-(a+b)+(a+2b)-(a+3b)+…+(a+100b)-(a+101b)
(1)试求:
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2014)(b+2014) |
(2)试求:a-(a+b)+(a+2b)-(a+3b)+…+(a+100b)-(a+101b)
考点:整式的加减—化简求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:规律型
分析:(1)已知等式利用非负数的性质求出a与b的值即可,将a与b的值代入原式拆项后,抵消合并即可得到结果;
(2)先去括号化简,然后将a、b的值代入即可.
(2)先去括号化简,然后将a、b的值代入即可.
解答:解:因为|a-2|+(1-b)2=0,且|a-2|≥0,(1-b)2≥0,
所以a-2=0,1-b=0,
所以a=2,b=1.
(1)原式=
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
;
(2)原式=a-a-b+a+2b-a-3b+…+a+100b-a-101b
=(a-a)+(a-a)+…+(a-a)+(2b-b)+(4b-3b)+…(100b-99b)+101b
=0+50b-101b
=-51b
=-51.
所以a-2=0,1-b=0,
所以a=2,b=1.
(1)原式=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2015×2016 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2015 |
| 1 |
| 2016 |
=1-
| 1 |
| 2016 |
=
| 2015 |
| 2016 |
(2)原式=a-a-b+a+2b-a-3b+…+a+100b-a-101b
=(a-a)+(a-a)+…+(a-a)+(2b-b)+(4b-3b)+…(100b-99b)+101b
=0+50b-101b
=-51b
=-51.
点评:此题考查了有理数的混合运算,熟练掌握运算法则,及正确将原式拆项是解本题的关键.

练习册系列答案
相关题目
设S=
+
+
+…+
,则4S的整数部分等于( )
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 399 |
| A、4 | B、2 | C、1 | D、0 |
 如图,在函数y=
如图,在函数y=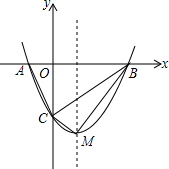 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点. 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|