题目内容
 在如图的四边形ABCD中,若∠A=90°,∠ADB=30°,AB=3,BC=10,CD=8,试求四边形ABCD的面积.
在如图的四边形ABCD中,若∠A=90°,∠ADB=30°,AB=3,BC=10,CD=8,试求四边形ABCD的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2AB,再利用勾股定理逆定理判断出△BCD是直角三角形,然后根据S四边形ABCD=S△ABD+S△BCD列式计算即可得解.
解答:解:在Rt△ABD中,∵∠A=90°,∠ADB=30°,AB=3,
∴BD=2AB=2×3=6,
∴AD=
=
=3
,
又∵BC=10,CD=8,
∴BD2+CD2=62+82=100,
而BC2=102=100,
∴BD2+CD2=BC2,
根据勾股定理的逆定理得△BCD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD,
=
AB•AD+
BD•BC,
=
×3×3
+
×6×8,
=
+24.
∴BD=2AB=2×3=6,
∴AD=
| BD2-AB2 |
| 62-32 |
| 3 |
又∵BC=10,CD=8,
∴BD2+CD2=62+82=100,
而BC2=102=100,
∴BD2+CD2=BC2,
根据勾股定理的逆定理得△BCD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
=
9
| ||
| 2 |
点评:本题考查了勾股定理,勾股定理逆定理,熟记定理并判断出△BCD是直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列长度的三条线段能组成直角三角形的是( )
A、1,1,
| ||
| B、2,3,4 | ||
| C、4,5,6 | ||
| D、6,8,11 |
通过尺规作图作一个角的平分线的理论依据是( )
| A、SAS | B、SSS |
| C、ASA | D、AAS |
已知x=2是一元二次方程x2+2ax+8=0的一个根,则a的值为( )
| A、1 | B、-1 | C、3 | D、-3 |

 把两个完全相同的矩形纸片ABCD,BFDE如图放置,已知AB=BF,求证:四边形BHDG是菱形.
把两个完全相同的矩形纸片ABCD,BFDE如图放置,已知AB=BF,求证:四边形BHDG是菱形.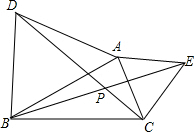 如图,已知△ABD和△AEC中,AD=AB,AE=AC,∠DAB=∠EAC=60°,CD、BE相交于点P.
如图,已知△ABD和△AEC中,AD=AB,AE=AC,∠DAB=∠EAC=60°,CD、BE相交于点P.