��Ŀ����
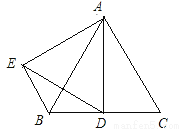
��ͼ��ʾ,�õ�A(3,1)��ʾ����3�����ܲ���1�����,��B(2,3)��ʾ����2�����ܲ���3�����.

(1)д����������C,D,E,F����ʾ������;
(2)��һֻ���Ӵ�A����B(˳�ŷ�������),�����¼���·����ѡ��:��A��C��D��B;��A��F��D��B;��A��F��E��B.��������·�Ե��ĺ��ܲ����?������·�Ե���������?
(1)��C��������(2,1),����ʾ�������Ƿ���2�����ܲ���1�����;��D��������(2,2),����ʾ�������Ƿ���2�����ܲ���2�����;��E��������(3,3),����ʾ�������Ƿ���3�����ܲ���3�����;��F��������(3,2),����ʾ�������Ƿ���3�����ܲ���2�����. (2)�ߵڢ���·�Ե��ĺ��ܲ�����˶����,���ɼ�����. ���������������: �ɵ�A�����꣨3��1������B�����꣨2��3������...��ͼ����ֱ������ƽ���ڣ���֪��A��8��0������B��3��0������C�ǵ�A����ֱ��m��ֱ��m�ϸ���ĺ����궼Ϊ3���ĶԳƵ㣮
��1����ͼ�б����A��B��C��λ�ò������C�����ꣻ
��2�������P��y���ϣ�����P��ֱ��l��x�ᣬ��A����ֱ��l�ĶԳƵ��ǵ�D����ô����BCD���������10ʱ�����P�����꣮
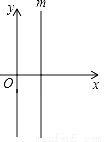
��һ��ֱ�����ǰ���ͼ�ڷţ�����ֱ�ǰ�ABC��б��BC�뺬30��ǵ�ֱ�����ǰ�DBE��ֱ�DZ�BD������ͬ����б��BC��BE��ͬһֱ���ϣ�AC��BD���ڵ�O������CD��
��֤����CDO�ǵ��������Σ�
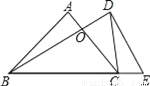
��ͼ����ABC�͡�ADE�ǵȱ������Σ�AD��BC���ϵ����ߣ���֤��BE=BD��
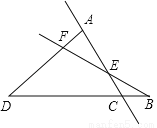
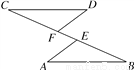
��ͼ����C��F��E��B��һ��ֱ���ϣ���CFD����BEA��CE��BF��DF��AE��д��CD��AB֮��Ĺ�ϵ����֤����Ľ��ۣ�
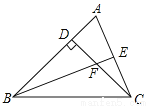
��ͼ���ڡ�ABC�У�CD��AB���ϸߣ�BEΪ��ƽ���ߣ�����BFC=113�㣬���BCF�Ķ�����
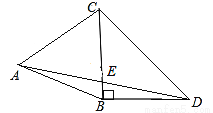
��ͼ����ABC�ǵȱ������Σ���CBD=90�㣬BD=BC������AD��BC�ڵ�E�����AEC�Ķ�����_________��
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������


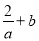 ��һ�ζ���ʽ
��һ�ζ���ʽ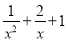 ���Ƕ���ʽ
���Ƕ���ʽ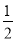 ��a��ϵ���ǣ�
��a��ϵ���ǣ�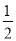
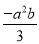 ��ϵ��Ϊ
��ϵ��Ϊ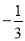 ������Ϊ3
������Ϊ3
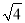 - 23��|- 2|��(- 7+5)=____.
- 23��|- 2|��(- 7+5)=____.