题目内容
3. 如图网格图中,每个小正方形的边长均为1,每个小格的顶点叫做格点.
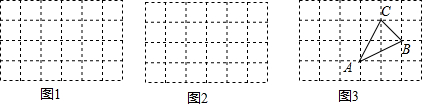
如图网格图中,每个小正方形的边长均为1,每个小格的顶点叫做格点.(1)请在图1中,画一个格点三角形,使它的三边长都是有理数;
(2)请在图2中,画一个格点三角形,使它的三边长都是无理数;
(3)图3中的△ABC的面积为$\frac{3}{2}$.
分析 由于正方形的边长为1,连接铬点的线段,可通过勾股定理计算出其边长.根据题目要求,3、4、5符合(1)要求的三角形,例如$\sqrt{2}$、3$\sqrt{2}$、2$\sqrt{5}$符合(2)要求的三角形.
(3)三角形的面积=矩形的面积-3个小直角三角形的面积.
解答  解:(1)(2)如右图所示.
解:(1)(2)如右图所示.
(3)三角形的面积=22-2×$1×\frac{1}{2}$-$\frac{1}{2}×1×1$-$\frac{1}{2}×2×1$
=$\frac{3}{2}$
故答案为:$\frac{3}{2}$
点评 本题考查了铬点三角形、勾股定理及三角形的面积公式.知道3、4、5能组成三角形,会把不规则的图形转化成规则图形求面积是解决本题的关键.

练习册系列答案
相关题目
 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.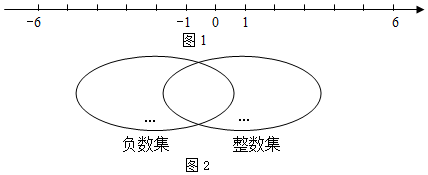 -4,|-2|,-2,-(-3.5),0,-1$\frac{1}{2}$
-4,|-2|,-2,-(-3.5),0,-1$\frac{1}{2}$ 如图,△ABC中,若DE∥AC,$\frac{BD}{AB}$=$\frac{1}{3}$,DE=4cm,则AC的长为12 cm.
如图,△ABC中,若DE∥AC,$\frac{BD}{AB}$=$\frac{1}{3}$,DE=4cm,则AC的长为12 cm.