Question

4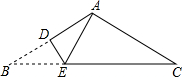．如图，△ABC是一张顶角为120°的三角形纸片，AB=AC，BC=6，现将△ABC折叠，使点B与点A 重合，折痕为DE，则DE的长为（　　）

• A． 1
• B． 2
• C． $2\sqrt{3}$
• D． 3

Answer 1

分析 作AH⊥BC于H，根据等腰三角形的性质求出BH，根据翻折变换的性质求出BD，根据正切的定义解答即可．

解答 解：作AH⊥BC于H，
∵AB=AC，AH⊥BC，
∴BH=$\frac{1}{2}$BC=3，
∵∠BAC=120°，AB=AC，
∴∠B=30°，
∴AB=$\frac{BH}{cos30°}$=2$\sqrt{3}$，
由翻折变换的性质可知，DB=DA=$\sqrt{3}$，
∴DE=BD•tan30°=1，
故选：A．

点评 本题考查的是翻折变换的性质、勾股定理的应用，翻折变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．