题目内容
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
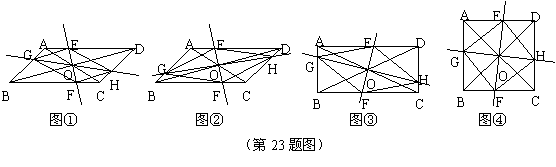 |
解:(1)四边形EGFH是平行四边形.
 证明:∵ ABCD的对角线AC、BD交于点O.
证明:∵ ABCD的对角线AC、BD交于点O.
 ∴点O是 ABCD的对称中心.
∴点O是 ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形.
(2)菱形.
(3)菱形.
(4)四边形EGFH是正方形.


 ∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.∵EF⊥GH ,∴∠GOF=90°.
∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.∵EF⊥GH ,∴∠GOF=90°.
∴∠BOG=∠COF.∴△BOG≌△COF.∴OG=OF,∴GH=EF.
由(1)知四边形EGFH是平行四边形,又∵EF⊥GH,EF=GH.
∴四边形EGFH是正方形.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
 C.1 D.
C.1 D.
 ,其中
,其中 .
. 介于( )
介于( ) B.
B. C.
C. D.
D.
 ,其中
,其中 .
.