题目内容
12.先化简:(1+$\frac{1}{x-2}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-4}$,再在不等式2x-9<0的解集中,选一个合适的数代入求值.分析 先根据分式混合运算的法则把原式进行化简,再求出x的取值范围,选取合适的x的值代入进行计算即可.
解答 解:原式=$\frac{x-1}{x-2}$•$\frac{(x+2)(x-2)}{(x-1)^{2}}$
=$\frac{x+2}{x-1}$,
解不等式2x-9<0得,x<$\frac{9}{2}$,
当x=3时,原式=$\frac{3+2}{3-1}$=$\frac{5}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
3.若x=2n+2n+2,y=2n-1+2n-3,其中n是整数,则x与y的数量关系是( )
| A. | x=8y | B. | y=8x | C. | x=4 y | D. | y=4 x |
1.某同学在计算某n边形的内角和时,不小心少输入一个内角,得到和为2005°.则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
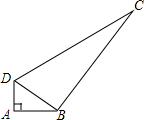 如图,在四边形ABCD中,∠BAD=90°,AD=1.5,AB=2,连接BD.
如图,在四边形ABCD中,∠BAD=90°,AD=1.5,AB=2,连接BD. 一块矩形场地,长为101米,宽为70米,从中留出如图所示的宽为1米的小道,其余部分种草,则草坪的面积为6900m2.
一块矩形场地,长为101米,宽为70米,从中留出如图所示的宽为1米的小道,其余部分种草,则草坪的面积为6900m2. 如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.
如图所示,△ABC沿射线XY的方向平移一定距离后成为△DEF,找出图中存在的平行且相等的三条线段是AD∥CF,AD=CF=BE.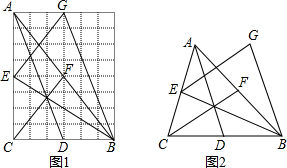 【阅读理解】
【阅读理解】 如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.