题目内容

2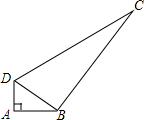．如图，在四边形ABCD中，∠BAD=90°，AD=1.5，AB=2，连接BD．
（1）求BD的长度；
（2）若BD⊥BC，CD=6.5，求四边形ABCD的面积．

分析 （1）在直角△ABD中，利用勾股定理来求线段BD的长度即可；
（2）根据勾股定理求得直角边BC的长度，然后根据图形得到四边形ABCD的面积=2个直角三角形的面积和．

解答 解：（1）∵如图，在四边形ABCD中，∠BAD=90°，AD=1.5，AB=2，
∴由勾股定理，得BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{1．{5}^{2}+{2}^{2}}$=2.5．

（2）∵BD⊥BC，
∴∠DBC=90°，
∴BC=$\sqrt{C{D}^{2}-B{D}^{2}}$=6，
∴S四边形ABCD=S△ABD+S△BCD=$\frac{1}{2}$AB×AD+$\frac{1}{2}$BC×BD=9．

点评 此题主要考查了勾股定理和勾股定理逆定理，把四边形的面积分解成两个直角三角形的面积来求是解本题的关键所在．

练习册系列答案
相关题目
12．已知一个十边形的每个内角都相等，那么这个十边形的内角度数是144°．
13．对x，y定义一种新运算T，规定：$T（x，y）=\frac{ax+by}{2x+y}$（其中a，b均为非零常数），这里等式右边是通常的四则运算，例如：$T（0，1）=\frac{a×0+b×1}{2×0+1}=b$，已知T（1，-1）=-2，T（4，2）=1
（1）求a，b的值；
（2）若关于m的不等式组$\left\{\begin{array}{l}T（2m，5-4m）≤4\\ T（m，3-2m）＞p\end{array}\right.$恰好有4个整数解，求实数p的取值范围．
10．下列计算错误的是（　　）
A．$\sqrt{14}×\sqrt{7}=7\sqrt{2}$B．$\sqrt{60}÷\sqrt{30}=\sqrt{2}$C．3$\sqrt{2}$$-\sqrt{2}$=3D．$\sqrt{9a}+\sqrt{25a}=8\sqrt{a}$
17．先化简，再求值：（$\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$）÷$\frac{{x}^{2}+2x}{{x}^{2}-1}$，其中x=$\sqrt{2}$．
7．代数式ad-bc可用符号$|\begin{array}{l}a{\;}^{\;}{\;}_{\;}b\\ c{\;}^{\;}{\;}_{\;}d\end{array}|$来表示，称之为二阶行列式．即$|\begin{array}{l}a{\;}^{\;}{\;}_{\;}b\\ c{\;}^{\;}{\;}_{\;}d\end{array}|=ad-bc$，用二阶行列式可以解二元一次方程组．由$\left\{\begin{array}{l}{a_1}x+{b_1}y={c_1}\\{a_2}x+{b_2}y={c_2}\end{array}\right.$得三个二阶行列式即$D=|\begin{array}{l}{a_1}{\;}^{\;}{b_1}\\{a_2}{\;}^{\;}{b_2}\end{array}|$，${D_x}=|\begin{array}{l}{c_1}{\;}^{\;}{b_1}\\{c_2}{\;}^{\;}{b_2}\end{array}|$及${D_y}=|\begin{array}{l}{a_1}{\;}^{\;}{c_1}\\{a_2}{\;}^{\;}{c_2}\end{array}|$那么方程组的解就是$\left\{\begin{array}{l}x=\frac{D_x}{D}\\ y=\frac{D_y}{D}\end{array}\right.$．
（1）求出二阶行列式$|\begin{array}{l}3{\;}^{\;}{\;}_{\;}5\\ 6{\;}^{\;}{\;}_{\;}4\end{array}|$的值；
（2）用二阶行列式解方程组$\left\{\begin{array}{l}3x+2y=-1\\ 5x-y-2=0\end{array}\right.$．
14．$\sqrt{2}-1$的相反数是1-$\sqrt{2}$，$\sqrt{2}-\sqrt{3}$的绝对值是$\sqrt{3}$-$\sqrt{2}$．
11．已知a是$\sqrt{5}$的整数部分，b是$\sqrt{5}$的小数部分，求2a-b．
12．先化简：（1+$\frac{1}{x-2}$）÷$\frac{{x}^{2}-2x+1}{{x}^{2}-4}$，再在不等式2x-9＜0的解集中，选一个合适的数代入求值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网