题目内容
9.2015年十一黄金周商场大促销,某店主计划从厂家采购高级羽绒服和时尚皮衣两种产品共20件,高级羽绒服的采购单价y1(元/件)与采购数量x1(件)满足y1=-20x1+1500(0<x1≤20,x1为整数);时尚皮衣的采购单价y2(元/件)与采购数量x2(件)满足y2=-10x2+1300(0<x2≤20,x2为整数).(1)经店主与厂家协商,采购高级羽绒服的数量不少于时尚皮衣数量,且高级羽绒服采购单价不低于1240元,问该店主共有几种进货方案?
(2)该店主分别以1760元/件和1700元/件的销售出高级羽绒服和时尚皮衣,且全部售完,则在(1)问的条件下,采购高级羽绒服多少件时总利润最大?并求最大利润.
分析 (1)首先根据题意求出x的取值范围,结合x为整数,即可判断出商家的几种进货方案;
(2)令总利润为W,根据利润=售价-成本列出W与x的函数关系式W=30(x-9)2+9570,求出二次函数的最值即可.
解答 解:(1)设购买羽绒服x件,则购买皮衣(20-x)件,则:
$\left\{\begin{array}{l}{x≥20-x}\\{-20x+150≥1240}\\{0<x≤20且x为整数}\end{array}\right.$,
∴10≤x≤13且为整数,
∴该店主有4种进货方案:
羽绒服10件,皮衣10件;
羽绒服11件,皮衣9件;
羽绒服12件,皮衣8件;
羽绒服13件,皮衣7件;
(2)设购买羽绒服x件,利润为W元,则
W=(1760+20x-1500)x+(1700+10(20-x)-1300)(20-x)
=30(x-9)2+9570(10≤x≤13且为整数)
∵a=30>0,
∴当10≤x≤13且为整数是,W随x的增大而增大,
∴当x=13时,最大利润为10050元.
答:当采购羽绒服13件时,有最大利润为10050元.
点评 本题主要考查二次函数的应用的知识点,解答本题的关键是明确销售单价与销售件数之间的函数关系式,会表达单件的利润及总利润,此题难度一般.

练习册系列答案
相关题目
20.下列几何体中,属于棱柱的是( )


| A. | ①③ | B. | ① | C. | ①③⑥ | D. | ①⑥ |
4.体育课上,全班男同学进行了100米测验,达标成绩为15秒,下表是某小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
问:(1)这个小组男生的达标率为多少?
(2)这个小组男生的平均成绩是多少秒?
| -0.87 | +1 | -1.2 | 0 | -0.7 | +0.6 | -0.4 | -0.1 |
(2)这个小组男生的平均成绩是多少秒?
1.若点P(b-3,-2b)在y轴上,则点P的坐标为( )
| A. | (0,-6) | B. | (-6,0) | C. | (0,6) | D. | (6,0) |
18.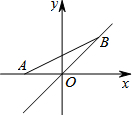 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
12.计算(-2x2y)2的结果是( )
| A. | -2x4y2 | B. | 4x4y2 | C. | -4x2y | D. | 4x4y |
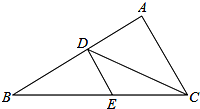 如图所示,在△ABC中,CD平分∠ACB,DE∥AC.
如图所示,在△ABC中,CD平分∠ACB,DE∥AC.