题目内容
15．
如图，在△ABC中，∠C=90°，AD平分∠CAB，BC=8cm，BD=5cm，那么点D到线段AB的距离是3cm．
分析 求D点到线段AB的距离，由于D在∠BAC的平分线上，只要求出D到AC的距离CD即可，由已知可用BC减去BD可得答案．
解答 解：CD=BC-BD，
=8cm-5cm=3cm，
∵∠C=90°，
∴D到AC的距离为CD=3cm，
∵AD平分∠CAB，
∴D点到线段AB的距离为3cm．
故答案为：3．
点评 本题考查了角平分线的性质；知道并利用CD是D点到线段AB的距离是正确解答本题的关键．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
5．下列说法正确的是（ ）
①正方体的截面可以是等边三角形，②正方体不可能截出七边形，③用一个平面截正方体，当这个平面与四个平面相交时，所得的截面一定是正方形，④正方体的截面中最多的是六边形．
①正方体的截面可以是等边三角形，②正方体不可能截出七边形，③用一个平面截正方体，当这个平面与四个平面相交时，所得的截面一定是正方形，④正方体的截面中最多的是六边形．
| A． | ①②③④ | B． | ①②③ | C． | ①③④ | D． | ①②④ |
6．
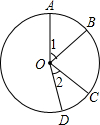如图，在⊙O中，$\widehat{AB}$=$\widehat{CD}$，∠1=45°，则∠2=（ ）
如图，在⊙O中，$\widehat{AB}$=$\widehat{CD}$，∠1=45°，则∠2=（ ）| A． | 60° | B． | 30° | C． | 45° | D． | 40° |
3．平面直角坐标系中，点A（-3，2），B（3，4），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（ ）
| A． | 6，（-3，4） | B． | 2，（3，2） | C． | 2，（3，0） | D． | 1，（4，2） |
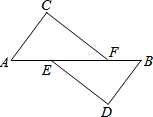已知，如图：A、E、F、B在一条直线上，AE=BF，∠C=∠B，CF∥DE，