题目内容
1.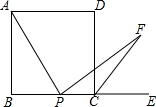 点E是正方形ABCD的边BC延长线上一点,点P是BC上任意一点,AP⊥PF,且AP=PF,连接CF.
点E是正方形ABCD的边BC延长线上一点,点P是BC上任意一点,AP⊥PF,且AP=PF,连接CF.(1)求证:∠BAP=∠FPC;
(2)求∠FCE的度数.
分析 (1)作FH⊥CE于H,则∠FHP=90°,先证出∠FPH=∠BAP,再由AAS证明△ABP≌△PHF,即可得出结论;
(2)由△ABP≌△PHF,得出BP=HF,AB=PH,证出BP=CH,得出CH=HF,即可求出结果.
解答 (1)证明:作FH⊥CE于H,则∠FHP=90°,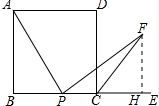
∵AP⊥PF,∴∠APF=90°,
∴∠APB+∠FPH=90°,
又∵∠BAP+∠APB=90°,
∴∠FPH=∠BAP,
∵四边形ABCD是正方形,
∴∠B=∠BCD=90°,AB=BC,
在△ABP和△PHF中,
$\left\{\begin{array}{l}{∠B=∠FHP=90°}&{\;}\\{∠BAP=∠FPH}&{\;}\\{AP=PF}&{\;}\end{array}\right.$,
∴△ABP≌△PHF(AAS),
∴∠BAP=∠FPC;
(2)解:∵△ABP≌△PHF,
∴BP=HF,AB=PH,
∴PH-PC=BC-PC,
∴BP=CH,
∴CH=HF.
∴∠FCE=∠CFH=$\frac{1}{2}$(180°-90°)=45°.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列选项中,∠MOP与∠NOP是邻补角的是( )
| A. |  | B. |  | C. |  | D. |  |
9.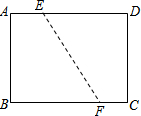 如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
 如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )
如图,矩形ABCD的边长AB=6,BC=8,将矩形沿EF折叠,使B点与D点重合,则折痕EF的长是( )| A. | 6 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{15}{2}$ |
 ,得( )
,得( ) B.
B.  C.
C.  D.
D. 
 ︱+(
︱+(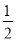 )-2;
)-2;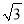 x-
x-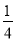 = 0.
= 0.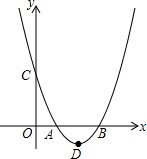 在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D.
在平面直角坐标系中,抛物线y1=ax2-4ax+n与x轴的交点A、B,抛物线的顶点为D. 已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于
已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于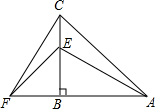 在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.
在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.