题目内容
 某小区要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水,连喷头在内,柱高为0.8m,水流各个方向上沿形状相同的抛物线路径落下,如图1所示.根据设计图纸已知:在图2,所示直角坐标系中水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+
某小区要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水,连喷头在内,柱高为0.8m,水流各个方向上沿形状相同的抛物线路径落下,如图1所示.根据设计图纸已知:在图2,所示直角坐标系中水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+| 4 |
| 5 |
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不考虑其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
考点:二次函数的应用
专题:
分析:本题是二次函数在实际问题中的运用,y表示水流喷出的高度,x表示水平距离,是二次函数关系,可以利用二次函数的性质解题.在求另外一个二次函数关系式时,确定函数关系式要充分运用条件“水流喷出的抛物线形状与(2)相同,喷头距水面0.35米”,求解析式.
解答:解:(1)y=-x2+2x+
=-(x-1)2+1.8.
答:喷出的水流距水面的最大高度为1.8米.
(2)当y=0时-x2+2x+
=0,
即(x-1)2=1.8,
解得x1=1+
,x2=1-
<0(舍去).
答:水池半径至少为(1+
)米.
| 4 |
| 5 |
答:喷出的水流距水面的最大高度为1.8米.
(2)当y=0时-x2+2x+
| 4 |
| 5 |
即(x-1)2=1.8,
解得x1=1+
3
| ||
| 5 |
3
| ||
| 5 |
答:水池半径至少为(1+
3
| ||
| 5 |
点评:本题考查二次函数的实际应用,根据实际问题求二次函数,再运用二次函数求最大值.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,那么∠DBC的度数为( )
如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,那么∠DBC的度数为( )| A、10° | B、15° |
| C、20° | D、30° |
 如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,若AB=CD=4,则梯形ABCD的周长为( )
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,若AB=CD=4,则梯形ABCD的周长为( )| A、16 | ||
| B、18 | ||
| C、20 | ||
D、12+4
|
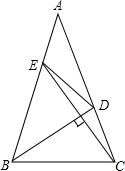 如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )
如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )| A、3个 | B、4个 | C、5个 | D、6个 |
两数-3
,2
的和比它们的相反数的和小( )
| 1 |
| 2 |
| 1 |
| 3 |
A、2
| ||
B、-2
| ||
C、1
| ||
D、-
|
 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 已知二次函数y=-x2+2bx的图象经过原点及x轴上正半轴另一点A,设此二次函数图象的顶点为B.
已知二次函数y=-x2+2bx的图象经过原点及x轴上正半轴另一点A,设此二次函数图象的顶点为B.