题目内容
已知:关于x的方程x2-4x+m=0.
(1)方程有实数根,求实数m的取值范围.
(2)若方程的一个根是1,求m的值及另一个根.
(1)方程有实数根,求实数m的取值范围.
(2)若方程的一个根是1,求m的值及另一个根.
考点:根的判别式,根与系数的关系
专题:
分析:(1)方程有实数根,则△≥0,建立关于m的不等式,求出m的取值范围.
(2)将x=1代入原方程即可求得m及另一根的值.
(2)将x=1代入原方程即可求得m及另一根的值.
解答:解:由题意知,△=16-4m≥0
∴m≤4.
∴当m≤4时,关于x的方程x2-4x+m=0有实数根;
(2)把x=1代入得:1-4+m=0,
解得:m=3,
将m=3代入得:x2-4x+3=0,解得:x=1或x=3,
故m=3,方程的另一根为3.
∴m≤4.
∴当m≤4时,关于x的方程x2-4x+m=0有实数根;
(2)把x=1代入得:1-4+m=0,
解得:m=3,
将m=3代入得:x2-4x+3=0,解得:x=1或x=3,
故m=3,方程的另一根为3.
点评:本题考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
计算(-2)2011×(0.5)2010等于( )
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
下列说法正确的是( )
| A、-a一定是负数 |
| B、两个数的和一定大于每一个加数 |
| C、若|m|=2,则m=±2 |
| D、若ab=0,则a=b=0 |
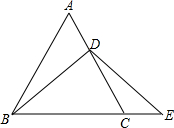 已知:△ABC是等边三角形,点D是线段AC上一点,作DB=ED,交BC延长线于点E.
已知:△ABC是等边三角形,点D是线段AC上一点,作DB=ED,交BC延长线于点E.