题目内容
13.先化简再求值(1)-2x2-$\frac{1}{2}$[3y2-2(x2-y2)+6],其中x=-1,y=2.
(2)$\frac{1}{2}$x-2(x-$\frac{1}{3}$y2)+($\frac{3}{2}$x+$\frac{1}{3}$y2),其中x,y满足|x-6|+(y+2)2=0.
分析 (1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;
(2)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:(1)原式=-2x2-$\frac{3}{2}$y2+x2-y2-3=-x2-$\frac{5}{2}$y2-3,
当x=-1,y=-2时,原式=-1-10-3=-14;
(2)原式=$\frac{1}{2}$x-2x+$\frac{2}{3}$y2+$\frac{3}{2}$x+$\frac{1}{3}$y2=y2,
∵|x-6|+(y+2)2=0,
∴x=6,y=-2,
则原式=4.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
8.已知y1=-x+5,y2=2x-1
(1)当x取何值时,y1=y2;
(2)当x取何值时,y1的值比y2的值的3倍大1;
(3)先填表,后回答:
根据所填表格,回答问题:随着x的值增大,y1的值逐渐减小;y2的值逐渐增大.
(1)当x取何值时,y1=y2;
(2)当x取何值时,y1的值比y2的值的3倍大1;
(3)先填表,后回答:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y1 | ||||||||
| y2 |
18.袋子中装有10个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则( )
| A. | 这个球一定是黑球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球可能是白球 | |
| D. | 事先能确定摸到什么颜色的球 |
2.下列各点中,在函数y=$\frac{2}{x}$的图象上的点是( )
| A. | (1,0.5) | B. | (2,-1) | C. | (-1,-2) | D. | (-2,1) |
 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求△DCE的面积.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求△DCE的面积.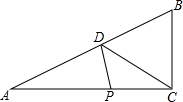 在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )
在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )


