题目内容
11．
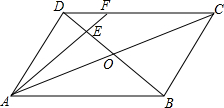如图，在平行四边形ABCD中，AC与BD相交于点O，E是OD的中点，连接AE并延长交DC于点F，则DF：FC=（ ）| A． | 1：4 | B． | 1：3 | C． | 1：2 | D． | 1：1 |
分析 首先证明△DFE∽△BAE，然后利用对应边成比例，E为OD的中点，求出DF：AB的值，又知AB=DC，即可得出DF：FC的值．
解答 解：在平行四边形ABCD中，AB∥DC，
则△DFE∽△BAE，
∴$\frac{DF}{AB}=\frac{DE}{EB}$，
∵O为对角线的交点，
∴DO=BO，
又∵E为OD的中点，
∴DE=$\frac{1}{4}$DB，
则DE：EB=1：3，
∴DF：AB=1：3，
∵DC=AB，
∴DF：DC=1：3，
∴DF：FC=1：2；
故选：C．
点评 本题考查了相似三角形的判定与性质以及平行四边形的性质，难度适中，解答本题的关键是根据平行证明△DFE∽△BAE，然后根据对应边成比例求值．
练习册系列答案
相关题目
如图，点A是双曲线y=$\frac{4}{x}$（x＜0）上一点，AO的延长线交双曲线y=$\frac{{k}^{2}}{x}$（x＞0，k＞0）于点B，BC⊥x轴，若S△ABC=7.5，则k的值为3．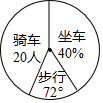
如图是七年级（21）班学生上学的不同方式的扇形统计图，若步行人数所占的圆心角的度数为72°，坐车的人数占40%，骑车人数为20人，则该班人数为50人．
如图所示，课外活动小组的同学剑豪与哲明利用所学知识区测量小河的宽度．剑豪同学在A处观测对岸C点，测得∠CAD=45°，哲明同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
3．下列分式是最简分式的是（ ）
| A． | $\frac{2a}{5{a}^{2}}$ | B． | $\frac{a}{5{a}^{2}-2a}$ | C． | $\frac{a-2b}{a+b}$ | D． | $\frac{ab-{b}^{2}}{{a}^{2}-{b}^{2}}$ |