��Ŀ����
3����ͼ1����Rt��ABC�У���C=90�㣬AC=BC=2����D��E�ֱ��ڱ�AC��AB�ϣ�AD=DE=$\frac{1}{2}$AB������DE������ADE�Ƶ�A��ʱ�뷽����ת������ת��Ϊ�ȣ���1�����ⷢ��
�ٵ���=0��ʱ��$\frac{BE}{CD}$=$\sqrt{2}$��
�ڵ���=180��ʱ��$\frac{BE}{CD}$=$\sqrt{2}$��
��2����չ̽��
���жϣ���0��ܦȣ�360��ʱ��$\frac{BE}{CD}$�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
��3��������
������ת�����У�BE�����ֵΪ2$\sqrt{2}$+2��
�ڵ���ADE��ת��B��D��E���㹲��ʱ���߶�CD�ij�Ϊ$\sqrt{3}$+1��$\sqrt{3}$-1��

���� ��1�������жϳ�DE��CB�������ó�����ʽ����ֵ���ɵó����ۣ�
���ȵó�DE��BC���ɵó���$\frac{AE}{AB}=\frac{AD}{AC}$�����ñ��������ʼ��ɵó����ۣ�
��2���ȡ�CAD=��BAE�������жϳ���ADC�ס�AEB���ɵó����ۣ�
��3���ֵ�D��BE���ӳ����Ϻ͵�D��BE�ϣ������ù��ɶ������BD���ٽ�����2�����ۼ��ɵó�CD��
��� �⣺��1���ٵ���=0��ʱ��
��Rt��ABC��AC=BC=2��
���A=��B=45�㣬AB=2$\sqrt{2}$��
��AD=DE=$\frac{1}{2}$AB=$\sqrt{2}$��
���AED=��A=45�㣬
���ADE=90�㣬
��DE��CB��
��$\frac{CD}{AC}=\frac{BE}{AB}$��
��$\frac{CD}{2}=\frac{BE}{2\sqrt{2}}$��
��$\frac{BE}{CD}=\sqrt{2}$��
�ʴ�Ϊ��$\sqrt{2}$��
�ڵ���=180��ʱ����ͼ1��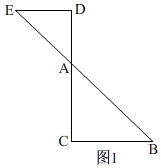
��DE��BC��
��$\frac{AE}{AB}=\frac{AD}{AC}$��
��$\frac{AE+AB}{AB}=\frac{AD+AC}{AC}$��
����$\frac{BE}{AB}=\frac{CD}{AC}$��
��$\frac{BE}{CD}=\frac{AB}{AC}$=$\frac{2\sqrt{2}}{2}$=$\sqrt{2}$��
�ʴ�Ϊ��$\sqrt{2}$��
��2����0��ܦȣ�360��ʱ��$\frac{BE}{CD}$�Ĵ�Сû�б仯��
���ɣ��ߡ�CAB=��DAE��
���CAD=��BAE��
��$\frac{AD}{AC}=\frac{AE}{AB}$��
���ADC�ס�AEB��
��$\frac{BE}{CD}=\frac{AB}{AC}$=$\frac{2\sqrt{2}}{2}$=$\sqrt{2}$��
��3���ٵ���E��BD���ӳ���ʱ��BE���
��Rt��ADE��AE=$\sqrt{2}$AD=2��
��BE���=AB+AE=2$\sqrt{2}$+2��
����ͼ2��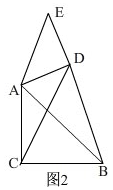
����E��BD��ʱ��
�ߡ�ADE=90�㣬
���ADB=90�㣬
��Rt��ADB�У�AB=2$\sqrt{2}$��AD=$\sqrt{2}$�����ݹ��ɶ����ã�DB=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{6}$��
��BE=BD+DE=$\sqrt{6}$+$\sqrt{2}$��
�ɣ�2��֪��$\frac{BE}{CD}=\sqrt{2}$��
��CD=$\frac{BE}{\sqrt{2}}$=$\frac{\sqrt{6}+\sqrt{2}}{\sqrt{2}}$=$\sqrt{3}$+1��
��ͼ3��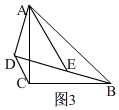
����D��BE���ӳ�����ʱ��
��Rt��ADB�У�AD=$\sqrt{2}$��AB=2$\sqrt{2}$�����ݹ��ɶ����ã�BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{6}$��
��BE=BD-DE=$\sqrt{6}$-$\sqrt{2}$��
�ɣ�2��֪��$\frac{BE}{CD}=\sqrt{2}$��
��CD=$\frac{BE}{\sqrt{2}}$=$\frac{\sqrt{6}-\sqrt{2}}{\sqrt{2}}$=$\sqrt{3}$-1��
�ʴ�Ϊ��$\sqrt{3}$+1��$\sqrt{3}$-1��
���� �������������ۺ��⣬��Ҫ�����˵���ֱ�������ε����ʺ��ж������ɶ��������������ε��ж������ʣ������Ļ������ʣ��⣨1���Ĺؼ��ǵó�DE��BC���⣨2���Ĺؼ����жϳ���ADC�ס�AEB���⣨3���ؼ�������ͼ�����BD����һ���е��Ѷȵ���Ŀ��

| ���� | һ | �� | �� | �� | �� | �� | �� |
| ���� | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
��2����������һ��Ȳ������ٵ�һ�������27 ����
��3�����ó�ʵ�а����������г������Ķ��ټƹ��ʣ����Ƽ������ƣ����ÿ����һ�����г��Ϳ��Ե������60Ԫ�������������ÿ��һ���ɶ��15Ԫ��������ƻ����ģ�ÿ������һ����15Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 4030 |
| A�� | ����-2x+6=8�������-2x=8+6 | |
| B�� | ����3+$\frac{8}{9}$x=6-3��x-1����ȥ���ŵã�3+$\frac{8}{9}$x=6-3x-1 | |
| C�� | ����ʽ$\frac{3x-1}{5}$-1��0��ȥ��ĸ�ã�3x-1-5��0 | |
| D�� | ����ʽ-$\frac{1}{2}$x��3����ã�x��-6 |
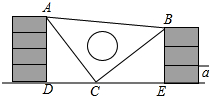 �μ䣬С��������ʦ�ĵ���ֱ�����ǰ��棬��С�ĵ�����ǽ֮�䣬��ͼ��ʾ��
�μ䣬С��������ʦ�ĵ���ֱ�����ǰ��棬��С�ĵ�����ǽ֮�䣬��ͼ��ʾ��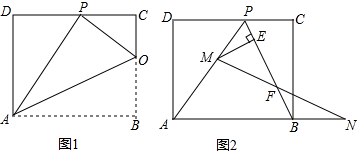
 д���������ɣ�
д���������ɣ�