题目内容
16．若a=$\frac{1}{\sqrt{2}-1}$，b=$\frac{1}{\sqrt{2}+1}$，则$\sqrt{ab}$（$\sqrt{\frac{a}{b}}$-$\sqrt{\frac{b}{a}}$）=2．分析 首先化简a，b，再化简原式，将a，b代入即可．
解答 解：a=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1，
b=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1，
$\sqrt{ab}$（$\sqrt{\frac{a}{b}}$-$\sqrt{\frac{b}{a}}$）=a-b，
将a=$\sqrt{2}$+1，b=$\sqrt{2}$-1代入得，
原式=a-b=$\sqrt{2}+1$$-（\sqrt{2}-1）$=2．
故答案为：2．
点评 本题主要考查了二次根式的化简，先化简再代入是解答此题的关键．
练习册系列答案
相关题目
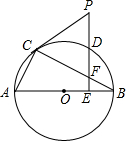如图，Rt△ABC内接于⊙O，D为BC中点，过点D作DE⊥AB于E，交BC于F，交过点C作⊙O的切线于点P．
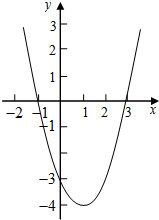阅读材料，解答问题．