题目内容
4.从-77起,逐次加1,得一列数:-77,-76,…,问:(1)第200个整数是多少?
(2)求这200个整数的和.
分析 (1)第2个整数为-77+1=-76;第3个整数为-76+1=-75;第4个整数为-75+1=-74,…依此类推第n个整数为-77+n-1=-78+n,故第200个整数为-78+200=122;
(2)100个整数之和为:-77+(-76)+(-75)+…+(-1)+0+1+…+122,找出互为相反数的两数之和为0,剩下的利用同号两数相加的法则计算,即可得到结果.
解答 解:(1)第200个整数为-78+200=122;
(2)这200个整数和为
-77+(-76)+(-75)+…+(-1)+0+1+…+122
=-(1+2+…+77)+(1+2+…+77)+(78+79+…+122)
=(122+78)×45÷2
=4500.
点评 此题考查了规律型:数字的变化类,其中得出规律第n个整数为-78+n是本题的突破点.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
9.下列各式中,与$\sqrt{x}$+$\sqrt{y}$互为有理化因式的是( )
| A. | a$\sqrt{x}$-b$\sqrt{y}$ | B. | b$\sqrt{x}$-a$\sqrt{y}$ | C. | $\sqrt{y}$-$\sqrt{x}$ | D. | $\sqrt{y}$+$\sqrt{x}$ |
 如图所示,有五个大小相同的正方形拼成“T“字形,试将它分成四块全等的图形.
如图所示,有五个大小相同的正方形拼成“T“字形,试将它分成四块全等的图形.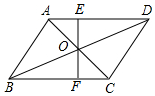 已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是32.
已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是32.
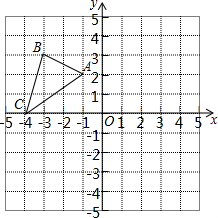 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.