题目内容
10.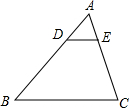 在△ABC中,DE∥BC,若$\frac{AD}{BD}=\frac{1}{2}$,
在△ABC中,DE∥BC,若$\frac{AD}{BD}=\frac{1}{2}$,(1)DE=4,求BC;
(2)△ABC的面积为18,求四边形DBEC的面积.
分析 (1)证明△ADE∽△ABC,根据相似三角形的对应边的比相等即可求解;
(2)根据相似三角形的面积的比等于相似比的平方即可求得△ADE的面积,则四边形的面积即可求解.
解答 解:(1)∵$\frac{AD}{BD}=\frac{1}{2}$,
∴$\frac{AD}{AB}$=$\frac{1}{3}$.
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{1}{3}$,即$\frac{4}{BC}$=$\frac{1}{3}$.
∴BC=12;
(2)∵△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=($\frac{1}{3}$)2=$\frac{1}{9}$.
即$\frac{{S}_{△ADE}}{18}$=$\frac{1}{9}$,
∴S△ADE=2,
∴S四边形DBEC=18-2=16.
点评 本题考查了相似三角形的判定与性质,相似三角形的对应边的比相等,相似三角形的面积的比等于相似比的平方.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
15.大、小两圆同心,环形面积是小圆面积的$\frac{a}{b}$倍,若大、小两圆的半径分别为R、r,则$\frac{R}{r}$等于( )
| A. | $\frac{\sqrt{a-b}}{\sqrt{b}}$ | B. | $\frac{\sqrt{a}}{\sqrt{a-b}}$ | C. | $\frac{\sqrt{b}}{\sqrt{a-b}}$ | D. | $\frac{\sqrt{a+b}}{\sqrt{b}}$ |
2. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )
 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,则下列结论错误的是( )| A. | △ADE≌△ADC | B. | DE=DC | C. | ∠ADE=∠ADC | D. | BD=DC |
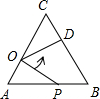 如图,在等边△ABC中,AC=9,点O在AC上,且AO=4,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是5.
如图,在等边△ABC中,AC=9,点O在AC上,且AO=4,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是5.