题目内容
18.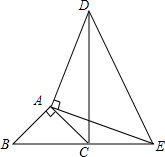 已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.
已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.(1)试证明:△BAE≌△CAD;
(2)说明CD与BE的位置关系并证明.
分析 (1)由已知可证AB=AC,AE=AD,∠BAC=∠EAD=90°,因为∠BAC+∠CAE=∠EAD+∠CAE,即可证∠BAE=∠CAD,符合SAS,即得证△BAE≌△CAD;
(2)根据全等三角形的性质解答即可.
解答 证明:(1)∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°,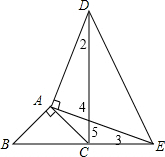 ∴∠BAC+∠CAE=∠EAD+∠CAE,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,
在△BAE与△CAD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AD=AE}\end{array}\right.$,
∴△BAE≌△CAD(SAS),
(2)如图,∵△BAE≌△CAD,
∴∠2=∠3,
∵∠4=∠5,
∴∠DAE=∠ACE=90°,
∴DC⊥BE.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
7.2015年10月17日是我国第二个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A、B两组捐款人数的比为1:5.
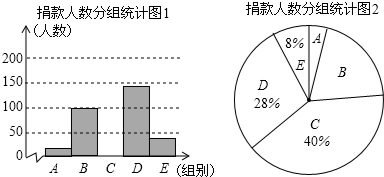
被调查的捐款人数分组统计表:
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?

被调查的捐款人数分组统计表:
| 组别 | 捐款额x/元 | 人数 |
| A | 1≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | 200 |
| D | 30≤x<40 | 140 |
| E | 40≤x | 40 |
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
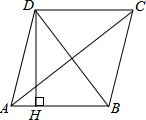 如图,四边形ABCD是菱形,AD=5,DB=6,DH⊥AB于H,则DH的长为$\frac{24}{5}$.
如图,四边形ABCD是菱形,AD=5,DB=6,DH⊥AB于H,则DH的长为$\frac{24}{5}$.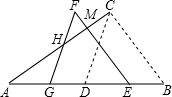 如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.
如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.