Question

如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连结DP交AC于点Q．

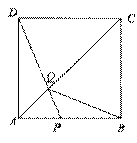
(1)试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；

(2)当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的；

(3)若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．

Answer 1

(1)证明：△ADQ≌△ABQ；

(2)以A为原点建立如图所示的直角坐标系，过点Q作QE⊥y轴于点E，QF⊥x轴于点F．

AD×QE＝S_{正方形ABCD}＝   ∴QE＝

∵点Q在正方形对角线AC上  ∴Q点的坐标为

∴过点D(0，4)，两点的函数关系式为：y＝－2x＋4，当y＝0时，x＝2，即P运动到AB中点时，△ADQ的面积是正方形ABCD面积的；

(3)若△ADQ是等腰三角形，则有QD＝QA或DA＝DQ或AQ＝AD

①当点P运动到与点B重合时，由四边形ABCD是正方形知  QD＝QA此时△ADQ是等腰三角形；

②当点P与点C重合时，点Q与点C也重合，此时DA＝DQ，△ADQ是等腰三角形；

③如图，设点P在BC边上运动到CP＝x时，有AD＝AQ

∵AD∥BC  ∴∠ADQ＝∠CPQ．

又∵∠AQD＝∠CQP，∠ADQ＝∠AQD，

∴∠CQP＝∠CPQ．

∴CQ＝CP＝x．

∵AC＝，AQ＝AD＝4．

∴x＝CQ＝AC－AQ＝－4．

即当CP＝－4时，△ADQ是等腰三角形．