题目内容
1.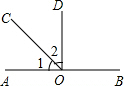 如图,点O在直线AB上,∠1=$\frac{1}{3}$∠BOC,OC是∠AOD的平分线;
如图,点O在直线AB上,∠1=$\frac{1}{3}$∠BOC,OC是∠AOD的平分线;(1)求:∠2的度数;
(2)试说明:OD⊥AB.
分析 (1)根据邻补角的定义列式求出∠AOC,再根据角平分线的定义可得∠COD=∠AOC;
(2)根据(1)的结论,求出∠AOD=90°,再根据垂直定义解答.
解答 解:(1)∵∠1=$\frac{1}{3}$∠BOC,∠1+∠BOC=180°,
∴∠1+3∠1=180°,
解得∠1=45°,
∵OC平分∠AOD,
∴∠2=∠1=45°;
(2)由(1)可得:
∠AOD=∠COD+∠AOC=45°+45°=90°,
∴OD⊥AB.
点评 本题考查了垂线的定义,邻补角的定义,角平分线的定义,根据邻补角的定义列式求出∠AOC是解题的关键.

练习册系列答案
相关题目
 如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.
如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.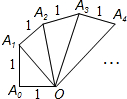 如图中的螺旋由一系列直角三角形组成,则第2017个三角形的面积为$\frac{\sqrt{2017}}{2}$.
如图中的螺旋由一系列直角三角形组成,则第2017个三角形的面积为$\frac{\sqrt{2017}}{2}$.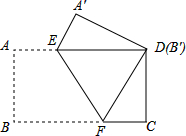 把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,AE=1,则AB=$\sqrt{3}$.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若∠DEF=60°,AE=1,则AB=$\sqrt{3}$.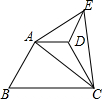 如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.
如图,将梯形ABCD沿直线AC翻折,点B落在点E处,联结ED,如果∠B=60°,∠ACB=40°,ED∥AB,那么∠AED的度数为20°.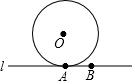 如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.