题目内容
 如图,?ABCD中,点F在CD上,AC与BF交于E,且CF:DF=1:2,则S△CEF:S?ABCD=
如图,?ABCD中,点F在CD上,AC与BF交于E,且CF:DF=1:2,则S△CEF:S?ABCD=考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:由四边形ABCD是平行四边形,可得△CEF∽△AEB,然后由相似三角形面积比等于相似比的平方,求得S△CEF:S△ABE=1:9,再设S△CEF=a,根据等高三角形的面积比等于对应底的比,可求得△ABC的面积,继而求得?ABCD的面积,则可求得答案.
解答:解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴△CEF∽△AEB,
∴CE:AE=CF:AB,
∵CF:DF=1:2,
∴CF:CD=CF:AB=1:3,
∴S△CEF:S△ABE=1:9,
设S△CEF=a,
则S△ABE=9a,
∵CE:AE=1:3,
∴S△ABE:S△BCE=3:1,
∴S△BCE=3a,
∴S△ABC=S△ABE+S△BCE=12a,
∴S?ABCD=2S△ABC=24a,
∴S△CEF:S?ABCD=1:24.
故答案为:1:24.
∴AB∥CD,AB=CD,
∴△CEF∽△AEB,
∴CE:AE=CF:AB,
∵CF:DF=1:2,
∴CF:CD=CF:AB=1:3,
∴S△CEF:S△ABE=1:9,
设S△CEF=a,
则S△ABE=9a,
∵CE:AE=1:3,
∴S△ABE:S△BCE=3:1,
∴S△BCE=3a,
∴S△ABC=S△ABE+S△BCE=12a,
∴S?ABCD=2S△ABC=24a,
∴S△CEF:S?ABCD=1:24.
故答案为:1:24.
点评:此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
用语言叙述
-3表示的数量关系中,表述不正确的是( )
| 1 |
| x |
| A、比x的倒数小3 |
| B、比x倒数大3的数 |
| C、x的倒数与3的差 |
| D、1除以x的商与3的差 |
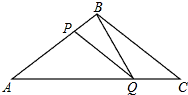 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿着AB以每秒4cm的速度向点B运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向点A运动.设运动时间为x.
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿着AB以每秒4cm的速度向点B运动;同时点Q从C点出发,沿着CA以每秒3cm的速度向点A运动.设运动时间为x. 如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.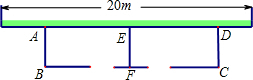 如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米.