题目内容
11.函数y=2x和y=ax+4的图象相交于点A(m,3),则关于x的不等式2x<ax+4的解集为( )| A. | x<$\frac{2}{3}$ | B. | x<$\frac{3}{2}$ | C. | x>-$\frac{3}{2}$ | D. | x<-$\frac{2}{3}$ |
分析 先把A(m,3)代入y=2x中解得m=$\frac{3}{2}$,再把把A($\frac{3}{2}$,3)代入y=ax+4中求出a=-$\frac{2}{3}$,然后解不等式2x<-$\frac{2}{3}$x+4即可.
解答 解:把A(m,3)代入y=2x得2m=3,解得m=$\frac{3}{2}$,
把A($\frac{3}{2}$,3)代入y=ax+4得3=$\frac{3}{2}$a+4,解得a=-$\frac{2}{3}$,
解不等式2x<-$\frac{2}{3}$x+4得x<$\frac{3}{2}$.
故选B.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
1.要使分式$\frac{{a}^{2}-9}{a+3}$的值为零,则a的值为( )
| A. | a=0 | B. | a=3 | C. | a=-3 | D. | a=±3 |
19. 如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
 如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.若a>b,则下列不等式变形错误的是( )
| A. | a+1>b+1 | B. | $\frac{a}{2}$>$\frac{b}{2}$ | C. | 4-3a>4-3b | D. | 3a-4>3b-4 |
20.若方程组$\left\{\begin{array}{l}{x-y=k+3}\\{2x+y=5k}\end{array}\right.$的解满足x+y<2,则k的取值范围是( )
| A. | k<-1 | B. | 1<k<2 | C. | k<1 | D. | -1<k<1 |
1.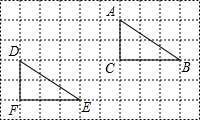 如图,在10×6的网格中,每个小正方形的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
如图,在10×6的网格中,每个小正方形的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
 如图,在10×6的网格中,每个小正方形的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
如图,在10×6的网格中,每个小正方形的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )| A. | 先向右平移5个单位,再向下平移2个单位 | |
| B. | 先向左平移5个单位,再向下平移2个单位 | |
| C. | 先向左平移5个单位,再向上平移2个单位 | |
| D. | 先向右平移5个单位,再向上平移2个单位 |