Question

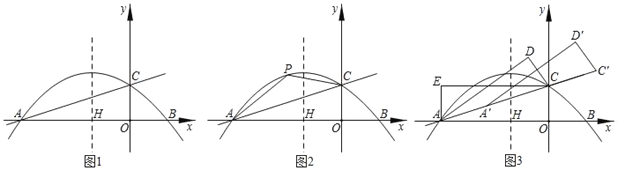
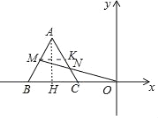
【题目】如图，在平面直角坐标系中，正△ABC的顶点B（﹣3，0）、C（﹣1，0），过坐标原点O的一条直线分别与边AB、AC交于点M、N．若OM＝2ON，则点N的坐标为_____．

Answer 1

【答案】

【解析】

作AH⊥BC于H，MK∥BC交AC于点K．由△MKN≌△OCN（AAS），推出MK＝OC＝1，KN＝NC，证明MK是△ABC的中位线即可解决问题；

解：如图，作AH⊥BC于H，MK∥BC交AC于点K．

∵B（﹣3，0）、C（﹣1，0），

∴BC＝2，

∵△ABC是等边三角形，

∴AB＝AC＝BC＝2，

∵AH⊥BC，

∴BH＝CH＝1，

∴AH＝，

∴A（﹣2，），

∵OM＝2ON，

∴MN＝ON，

∵MK∥OB，

∴∠MKN＝∠CON，

∵∠MNK＝∠CNO，

∴△MKN≌△OCN（AAS），

∴MK＝OC＝1，KN＝NC，

∵MK＝BC，MK∥BC，

∴MK是△ABC的中位线，

∴AK＝CK，

∴K，

∵KN＝CN，

∴N，

故答案为．