Question

【题目】如图，四边形ABCD为圆内接四边形，A为弧BD中点，连接对角线AC，E在AC上，且AE＝AB求证：

（1）∠CBE＝∠CAD；

（2）AC2＝BCCD+AB2．

Answer 1

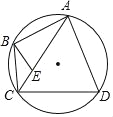
【答案】（1）证明见解析 （2）证明见解析

【解析】

（1）连接BD交AC于F，根据圆的性质得：∠ABD＝∠ACB＝∠ACD，由等腰三角形的性质得：∠ABE＝∠AEB，根据外角的性质得：∠CBE＝∠DBE，从而得结论；

（2）先根据两角相等两三角形相似证明：△ACD∽△BCF和△ABF∽△ACB，列比例式后，化为乘积式后相加可得结论．

证明：（1）连接BD交AC于F，

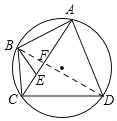
∵A为弧BD中点，

∴弧AB=弧AD，

∴∠ABD＝∠ACB＝∠ACD，

∵AB＝AE，

∴∠ABE＝∠AEB，

∵∠AEB＝∠ACB+∠CBE，∠ABE＝∠ABD+∠DBE，

∴∠CBE＝∠DBE，

∵∠CAD＝∠CBD＝2∠CBE，

∴∠CBE＝∠CAD，

（2）∵∠DBC＝∠CAD，∠ACB＝∠ACD，

∴△ACD∽△BCF，

∴ ，

∴BCCD＝ACCF①，

∵∠ABF＝∠ACB，∠BAF＝∠CAB，

∴△ABF∽△ACB，

∴，

∴AB2＝ACAF②，

①+②得：AB2+BCCD＝ACCF+ACAF＝AC（CF+AF），

∴AC2＝BCCD+AB2．