��Ŀ����
����Ŀ����֪������y����![]() x2��
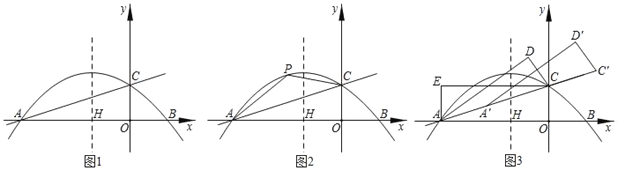
x2��![]() x+2��x�ύ�ڵ�A��B���㣬��y����C�㣬�����ߵĶԳ�����x�ύ��H�㣬�ֱ���OC��OAΪ��������AECO��
x+2��x�ύ�ڵ�A��B���㣬��y����C�㣬�����ߵĶԳ�����x�ύ��H�㣬�ֱ���OC��OAΪ��������AECO��
��1����ֱ��AC�Ľ���ʽ��
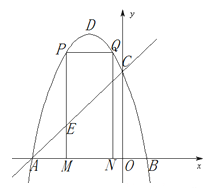
��2����ͼ2��PΪֱ��AC�Ϸ��������ϵ�����һ�㣬�ڶԳ�������һ����M�����ı���AOCP������ʱ����|PM��OM|�����ֵ��
��3����ͼ3������AOC��ֱ��AC���۵á�ACD���ٽ���ACD����ֱ��ACƽ�Ƶá�A'C��D'��ʹ�õ�A�䡢C'��ֱ��AC�ϣ��Ƿ���������ĵ�D�䣬ʹ�á�A��ED��Ϊֱ�������Σ������ڣ��������D������ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y��![]() x+2��(2) ��M����Ϊ����2��
x+2��(2) ��M����Ϊ����2��![]() ��ʱ���ı���AOCP��������ʱ|PM��OM|�����ֵ
��ʱ���ı���AOCP��������ʱ|PM��OM|�����ֵ![]() �� (3)���ڣ�D������Ϊ����0��4����6��2����
�� (3)���ڣ�D������Ϊ����0��4����6��2����![]() ��
��![]() ����
����
��������
��1����x��0����y��2����y��0����x��2��6�������A��B��C���������������
��2������OP���Գ����ڵ�M����ʱ��|PM��OM|�����ֵ�����������
��3������������A��D���A��E����A��D���ED�䣻��ED���A��E����������ù��ɶ����з�����⼴����
��1����x��0����y��2����y��0����x��2��6����A����6��0����B��2��0����C��0��2���������Գ���Ϊ��x����2����������Ϊ����2��![]() ����C������Ϊ��0��2���������C��ֱ�߱���ʽΪ��y��kx+2������A���������ʽ�������k
����C������Ϊ��0��2���������C��ֱ�߱���ʽΪ��y��kx+2������A���������ʽ�������k![]() ������ֱ��AC�ı���ʽΪ��y
������ֱ��AC�ı���ʽΪ��y![]() x+2��
x+2��
��2����ͼ������P��x��Ĵ��߽�AC�ڵ�H��

�ı���AOCP�������AOC�����+��ACP��������ı���AOCP������ʱ��ֻ��Ҫ��ACP�������������P����Ϊ��m��![]() m2
m2![]() m+2�������G������m��
m+2�������G������m��![]() m+2����S��ACP
m+2����S��ACP![]() PGOA
PGOA![]() ��
��![]() m2
m2![]() m+2
m+2![]() m��2��6
m��2��6![]() m2��3m����m����3ʱ����ʽȡ�����ֵ�����P����Ϊ����3��
m2��3m����m����3ʱ����ʽȡ�����ֵ�����P����Ϊ����3��![]() ��������OP���Գ����ڵ�M����ʱ��|PM��OM|�����ֵ��ֱ��OP�ı���ʽΪ��y
��������OP���Գ����ڵ�M����ʱ��|PM��OM|�����ֵ��ֱ��OP�ı���ʽΪ��y![]() x����x����2ʱ��y
x����x����2ʱ��y![]() ��������M����Ϊ����2��
��������M����Ϊ����2��![]() ����|PM��OM|�����ֵΪ��
����|PM��OM|�����ֵΪ��![]() =
=![]() ��
��
��3��������

��AE��CD����AEC����ADC��90�㣬��EMA����DMC�����EAM�ա�DCM��AAS������EM��DM��AM��MC������EM��a������MC��6��a����Rt��DCM�����ɹ��ɶ�������MC2��DC2+MD2��������6��a��2��22+a2�������a![]() ������MC
������MC![]() ������D��x��Ĵ��߽�x���ڵ�N����EC�ڵ�H����Rt��DMC����
������D��x��Ĵ��߽�x���ڵ�N����EC�ڵ�H����Rt��DMC����![]() DHMC
DHMC![]() MDDC������DH
MDDC������DH![]() 2������DH
2������DH![]() ��HC
��HC![]() ��������D��������
��������D��������![]() ����
����
������ACD����ֱ��ACƽ����m����λ��������A�����꣨��6![]() ������D������Ϊ��
������D��������![]() ��������E��������6��2������
��������E��������6��2������![]() =
=![]() =36��
=36��![]() =
=![]() =
=![]() ��
��![]() =
=![]() =
=![]() ������A��ED��Ϊֱ�������Σ�������������ۣ�
������A��ED��Ϊֱ�������Σ�������������ۣ�
�ٵ�![]() +
+![]() =
=![]() ʱ��36+
ʱ��36+![]() =
=![]() �������m=
�������m=![]() ����ʱD�䣨
����ʱD�䣨![]() ��Ϊ��0��4����
����0��4����
����![]() +
+![]() =
=![]() ʱ��36+
ʱ��36+![]() =
=![]() �������m=
�������m=![]() ����ʱD�䣨
����ʱD�䣨![]() ��Ϊ����6��2����
������6��2����
����![]() +
+![]() =
=![]() ʱ��
ʱ��![]() +
+![]() =36�������m=
=36�������m=![]() ��m=
��m=![]() ����ʱD�䣨
����ʱD�䣨![]() ��Ϊ����6��2����
������6��2����![]() ��
��![]() ����
����
����������D��������0��4����6��2����![]() ��
��![]() ����
����

 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�