题目内容
19.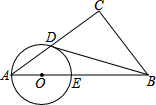 已知:如图所示,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A,求证:BD与⊙O相切.
已知:如图所示,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A,求证:BD与⊙O相切.
分析 连接OD,结合条件可证得∠CBD+∠BDC=90°,可得∠ODB=90°,则可证得结论.
解答  证明:
证明:
连接OD,
∵OA=OD,
∴∠ODA=∠A=∠CBD,
∵∠C=90°,
∴∠ODA+∠BDC=∠CBD+∠BDC=90°,
∴∠ODB=90°,即OD⊥BD,
∴BD与⊙O相切.
点评 本题主要考查切线的判定,掌握切线的判定方法是解题的关键,即有切点时连接圆心和切点,证明垂直,无切点时,作距离证明距离等于半径.

练习册系列答案
相关题目
10.下列说法中错误的是( )
| A. | 有理数可以分为正有理数、负有理数和零 | |
| B. | 0的相反数等于它本身 | |
| C. | 0既不是正数也不是负数 | |
| D. | 任何一个有理数的绝对值都是正数 |
11.教练从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛,两人在相同条件下各打了5发子弹,命中环数如下:甲:9,8,7,7,9;乙:10,9,8,7,6.应选( )参加.
| A. | 甲 | B. | 乙 | C. | 甲、乙都可以 | D. | 无法确定 |
9.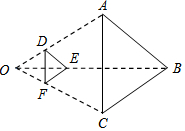 如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
 如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )| A. | 2S | B. | 3S | C. | 4S | D. | 9S |
 如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B=95°.
如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B=95°.