题目内容
若n(n≠0)是关于x的方程x2+mx+3n=0的一个根,则m+n的值是 .
=3 .
【考点】一元二次方程的解.
【分析】根据一元二次方程的解的定义得到n2+mn+3n=0,然后两边除以n即可得到m+n的值.
【解答】解:把x=n代入x2+mx+3n=0得n2+mn+3n=0,
∵n≠0,
∴n+m+3=0,
即m+n=﹣3.
故答案是:﹣3.
【点评】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
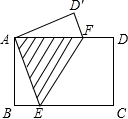

 x2+
x2+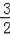

 B.
B.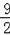
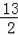
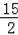

 D.
D.
