题目内容
16.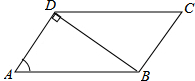 如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
分析 先由三角函数求出BD,再根据勾股定理求出AD,?ABCD的面积=AD•BD,即可得出结果.
解答 解:∵AD⊥BD,
∴∠ADB=90°,
∵AB=4,sinA=$\frac{3}{4}$,
∴BD=AB•sinA=4×$\frac{3}{4}$=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴?ABCD的面积=AD•BD=3$\sqrt{7}$;
故答案为:3$\sqrt{7}$.
点评 本题考查了平行四边形的性质、三角函数、勾股定理以及平行四边形面积的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
11.多项式mx2-m与多项式x2-2x+1的公因式是( )
| A. | x-1 | B. | x+1 | C. | x2-1 | D. | (x-1)2 |
1.下列等式中,正确的是( )
| A. | 3a-2a=1 | B. | a2•a3=a5 | C. | (-2a3)2=-4a6 | D. | (a-b)2=a2-b2 |
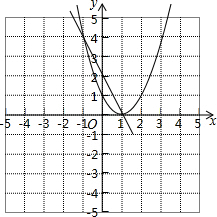 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
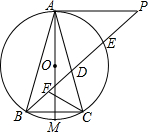 如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC 如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为5.
如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为5.