题目内容
5. 如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为5.
如图,△ABC中,D为BC上一点,∠BAD=∠C,AB=6,BD=4,则CD的长为5.
分析 易证△BAD∽△BCA,然后运用相似三角形的性质可求出BC,从而可得到CD的值.
解答 解:∵∠BAD=∠C,∠B=∠B,
∴△BAD∽△BCA,
∴$\frac{BA}{BC}$=$\frac{BD}{BA}$.
∵AB=6,BD=4,
∴$\frac{6}{BC}$=$\frac{4}{6}$,
∴BC=9,
∴CD=BC-BD=9-4=5.
故答案为5.
点评 本题主要考查的是相似三角形的判定与性质,由角等联想到三角形相似是解决本题的关键.

练习册系列答案
相关题目
15.如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是( )
| A. | y=x2-1 | B. | y=x2+6x+5 | C. | y=x2+4x+4 | D. | y=x2+8x+17 |
17.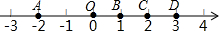 如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-$\sqrt{5}$的点P应落在线段( )
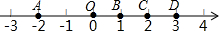 如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、C、D分别表示数-2、1、2、3,则表示数3-$\sqrt{5}$的点P应落在线段( )| A. | AO上 | B. | OB上 | C. | BC上 | D. | CD上 |
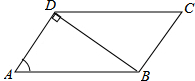 如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4,sinA=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.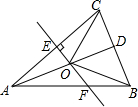 如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )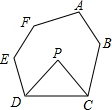 如图,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠DCB,则∠P与∠A+∠B+∠E+∠F的数量关系可表示为∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
如图,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠DCB,则∠P与∠A+∠B+∠E+∠F的数量关系可表示为∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°. 如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以
如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以