题目内容
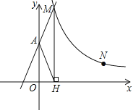
【题目】如图,直线![]() 与
与![]() 轴交于
轴交于![]() 点,与反比例函数
点,与反比例函数![]() 的图象交于点
的图象交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,且
,且![]()
![]() 求
求![]() 的值;
的值;
![]() 点
点![]() 是反比例函
是反比例函![]() 图象上的点,在
图象上的点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 最小?若存在,求出点
最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)4;(2)存在,点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)先求出A点坐标,从而得到H的横坐标,即M的横坐标,然后代入直线解析式求得纵坐标,再利用待定系数法求得k的值;
(2)存在,先求出N点的坐标,作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连结
,连结![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小,然后用待定系数法求得直线
最小,然后用待定系数法求得直线![]() 的解析式,再求出其与x轴的交点即可.
的解析式,再求出其与x轴的交点即可.
解:![]() ∵直线
∵直线![]() 与
与![]() 轴交于
轴交于![]() 点,
点,
∴![]() 点坐标为
点坐标为![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,
∴![]() 点横坐标为
点横坐标为![]() ,
,
∵点![]() 在直线
在直线![]() 上,
上,
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ;
;
![]() 存在.
存在.
∵点![]() 是反比例函
是反比例函![]() 图象上的点,
图象上的点,
∴![]() ,即点
,即点![]() ,
,

作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连结
,连结![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小;
最小;
∵![]() 与
与![]() 关于
关于![]() 轴,点
轴,点![]() ,
,
∴点![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,解得
,解得 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目