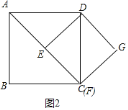
题目内容
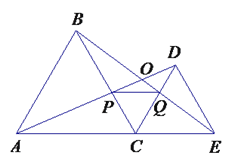
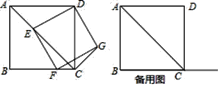
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:矩形
,求证:矩形![]() 是正方形;
是正方形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
![]() 当线段
当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,直接写出
时,直接写出![]() 的度数.
的度数.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)作EP⊥CD于P,EQ⊥BC于Q,根据已知条件结合图形易证Rt△EQF≌Rt△EPD,根据全等三角形的性质可得EF=ED,根据正方形的判定定理即可证得结论;(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解答;(3)分①![]() 与
与![]() 的夹角为
的夹角为![]() 和②
和②![]() 与
与![]() 的夹角为
的夹角为![]() 时两种况解答即可.
时两种况解答即可.
![]() 证明:作
证明:作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴矩形![]() 是正方形;
是正方形;
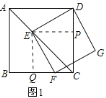
![]() 如图
如图![]() 中,在
中,在![]() 中.
中.![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() 与
与![]() 重合,此时
重合,此时![]() 是等腰直角三角形,易知
是等腰直角三角形,易知![]() .
.
![]() ①当
①当![]() 与
与![]() 的夹角为
的夹角为![]() 时,
时,![]() ,
,
②当![]() 与
与![]() 的夹角为
的夹角为![]() 时,
时,![]()
综上所述,![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目