Question

19．如图所示，在△ABC中，已知AB=AC=17，BC=16，请你根据上述数据求AB边上的高．

Answer 1

分析 利用等腰三角形的性质求得BD=$\frac{1}{2}$BC=8cm．然后在直角△ABD中，利用勾股定理来求AD的长度，最后用面积法求出AB边上的高，

解答 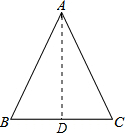解：如图，作AD⊥BC于点D，
∵△ABC中，AB=AC=17，BC=16，
∴BD=$\frac{1}{2}$BC=8，
∴在直角△ABD中，由勾股定理，得
AD=$\sqrt{1{7}^{2}-{8}^{2}}$=15（cm）．
∴S_△ABC=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×16×15=120，
设AB边上的高为h，
∴S_△ABC=$\frac{1}{2}$AB×h=$\frac{1}{2}$×17h=120，
∴h=$\frac{240}{17}$cm．
即：AB边上的高为$\frac{240}{17}$．

点评 此题主要考查了勾股定理，等腰三角形的性质的理解及运用．利用等腰三角形“三线合一”的性质求得BD是关键．