题目内容
 如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD.
如图,⊙O是△ABC的外接圆,点I是△ABC的内心,延长AI交⊙O于点D,交BC于点E,连接BD.(1)线段BD与ID相等吗?证明你的结论.
(2)证明:ID2=DE•AD.
考点:三角形的内切圆与内心,相似三角形的判定与性质
专题:
分析:(1)连接BI,证∠BIED∠IBD即可;∠IBD=∠4+∠5,∠BID=∠2+∠3;观察上述两个式子:I是△ABC的内心,则∠3=∠4,∠1=∠2;而∠1=∠5,由此可得∠5=∠2;即∠BID=∠IBD,由此得证;
(2)由(1)知:ID=BD,即证BE是哪两条线段的比例中项,可通过找以BD为公共边的相似三角形;由(1)证得∠5=∠2,易证得△BED∽△ABD,由此可得出所求的结论.
(2)由(1)知:ID=BD,即证BE是哪两条线段的比例中项,可通过找以BD为公共边的相似三角形;由(1)证得∠5=∠2,易证得△BED∽△ABD,由此可得出所求的结论.
解答: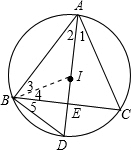 解:(1)ID=BD,
解:(1)ID=BD,
理由:∵I是△ABC的内心,
∴∠1=∠2,∠3=∠4;
∵∠BID=∠3+∠2,∠DBI=∠4+∠5,且∠5=∠1,
∴∠BID=∠DBI;
∴ID=BD;
(2)证明:如图所示:
∵∠5=∠1,∠1=∠2;
∴∠5=∠2;
又∵∠D=∠D,
∴△BDE∽△ADB;
∴BD:DE=AD:BD;
∴BD2=AD•DE;
又∵ID=BD,
∴ID2=AD•DE.
 解:(1)ID=BD,
解:(1)ID=BD,理由:∵I是△ABC的内心,
∴∠1=∠2,∠3=∠4;
∵∠BID=∠3+∠2,∠DBI=∠4+∠5,且∠5=∠1,
∴∠BID=∠DBI;
∴ID=BD;
(2)证明:如图所示:
∵∠5=∠1,∠1=∠2;
∴∠5=∠2;
又∵∠D=∠D,
∴△BDE∽△ADB;
∴BD:DE=AD:BD;
∴BD2=AD•DE;
又∵ID=BD,
∴ID2=AD•DE.
点评:本题考查了三角形的内切圆和内心的以及等腰三角形的判定与性质,同弧所对的圆周角相等,得出△BDE∽△ADB是解题关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
下列方程是一元一次方程的是( )
| A、x-3y=4 | ||
| B、xy=4 | ||
C、
| ||
D、3y-
|
将抛物线y=-2x2+1向右平移1个单位,再向下平移3个单位后所得到的抛物线为( )
| A、y=-2(x+1)2-2 |
| B、y=-2(x+1)2-4 |
| C、y=-2(x-1)2-2 |
| D、y=-2(x-1)2-4 |
 小明同学想测量妈妈佩戴的玉手镯的半径,他只有一把直尺和一块三角板,他将直尺、玉手镯和三角板如图放置于桌面上并量出AB=2cm,则此手镯的半径OB是多少cm?
小明同学想测量妈妈佩戴的玉手镯的半径,他只有一把直尺和一块三角板,他将直尺、玉手镯和三角板如图放置于桌面上并量出AB=2cm,则此手镯的半径OB是多少cm?