题目内容
 将一张腰长为5cm的等腰直角三角形的纸片折起,使直角顶点B恰好落在斜边AC上的D处,求折叠后三角形DEC的面积.
将一张腰长为5cm的等腰直角三角形的纸片折起,使直角顶点B恰好落在斜边AC上的D处,求折叠后三角形DEC的面积.考点:翻折变换(折叠问题)
专题:
分析:根据等腰直角三角形的性质求出AC,∠C=45°,再根据翻折变换的性质可得AD=AB,∠ADE=∠B=90°,然后判断出△CDE是等腰直角三角形,根据等腰直角三角形的面积公式列式计算即可得解.
解答:解:∵△ABC是等腰直角三角形,
∴AC=
AB=5
cm,∠C=45°,
∵翻折后直角顶点B恰好落在斜边AC上的D处,
∴AD=AB=5cm,∠ADE=∠B=90°,
∴△CDE是等腰直角三角形,
∴△DEC的面积=
CD2=
(5
-5)2=
cm2.
∴AC=
| 2 |
| 2 |
∵翻折后直角顶点B恰好落在斜边AC上的D处,
∴AD=AB=5cm,∠ADE=∠B=90°,
∴△CDE是等腰直角三角形,
∴△DEC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
75-50
| ||
| 2 |
点评:本题考查了翻折变换的性质,等腰直角三角形的性质,熟记各性质并求出△CDE是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
 如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则: 如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,若AC⊥BD,AD=3,S梯形ABCD=16,则AB的长为
如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,若AC⊥BD,AD=3,S梯形ABCD=16,则AB的长为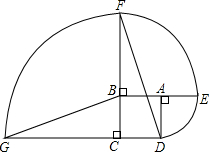 如图,ABCD是边长为1的正方形,其中
如图,ABCD是边长为1的正方形,其中