题目内容
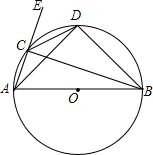 如图,⊙O的直径AB长为6,弦AC长为2,点E在AC的延长线上,∠ECB的平分线交⊙O于点D,求BC和AD的长.
如图,⊙O的直径AB长为6,弦AC长为2,点E在AC的延长线上,∠ECB的平分线交⊙O于点D,求BC和AD的长.考点:圆周角定理,勾股定理,等腰直角三角形
专题:
分析:根据圆周角定理由AB为⊙O的直径得到∠ACB=∠ADB=90°,在Rt△ACB中,利用勾股定理可计算出BC=4
,再利用DC平分∠ECB得到∠DCB=45°,根据圆周角定理得∠DAB=∠DCB=45°,然后根据等腰直角三角形的性质计算AD.
| 2 |
解答:解:∵AB为⊙O的直径,
∴∠ACB=90°,∠ADB=90°,
在Rt△ACB中,
∵AB=6,AC=2,
∴BC=
=4
;
∵DC平分∠ECB,
∴∠DCB=45°,
∴∠DAB=∠DCB=45°,
∴△ABD为等腰直角三角形,
∴AD=
AB=
×6=3
.
∴∠ACB=90°,∠ADB=90°,
在Rt△ACB中,
∵AB=6,AC=2,
∴BC=
| AB2-AC2 |
| 2 |
∵DC平分∠ECB,
∴∠DCB=45°,
∴∠DAB=∠DCB=45°,
∴△ABD为等腰直角三角形,
∴AD=
| ||
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.会利用勾股定理和等腰直角三角形的性质进行计算.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
如果x≠0,那么
+6x
-
-x2
的值是( )
| 5 |
| 3 |
| 9x |
|
| x3 |
|
| A、负数 | B、正数 |
| C、非负数 | D、需要加以讨论 |
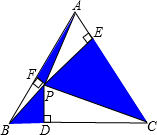 如图,P为边长为2的正三角形中任意一点,连接PA、PB、PC.过P点分别作三边的垂线,垂足分别为D、E、F,则PD+PE+PF=
如图,P为边长为2的正三角形中任意一点,连接PA、PB、PC.过P点分别作三边的垂线,垂足分别为D、E、F,则PD+PE+PF=