题目内容
用公式法解方程:
(1)x2+x-6=0
(2)x2-
x-
=0
(3)3x2-6x-2=0
(4)4x2-6x=0
(5)x2+4x+8=4x+11.
(1)x2+x-6=0
(2)x2-
| 3 |
| 1 |
| 4 |
(3)3x2-6x-2=0
(4)4x2-6x=0
(5)x2+4x+8=4x+11.
考点:解一元二次方程-公式法
专题:计算题
分析:方程先化为一般式,再计算判别式的值,然后利用求根公式求解.
解答:解:(1)△=12-4×1×(-6)=25,
x=
=
,
所以x1=2,x2=-3;
(2)△=(
)2-4×1×(-
)=4,
x=
,
所以x1=
,x2=
;
(3)△=(-6)2-4×3×(-2)=60,
x=
=
,
所以x1=
,x2=
;
(4))△=(-6)2-4×4×0=36,
x=
,
所以x1=0,x2=
;
(5)x2-3=0,
△=02-4×1×(-3)=12,
x=
=±
,
所以x1=
,x2=-
.
x=
-1±
| ||
| 2 |
| -1±5 |
| 2 |
所以x1=2,x2=-3;
(2)△=(
| 3 |
| 1 |
| 4 |
x=
| ||
| 2 |
所以x1=
| ||
| 2 |
| ||
| 2 |
(3)△=(-6)2-4×3×(-2)=60,
x=
6±
| ||
| 2×3 |
3±
| ||
| 3 |
所以x1=
3+
| ||
| 3 |
3-
| ||
| 3 |
(4))△=(-6)2-4×4×0=36,
x=
| 6±6 |
| 2×4 |
所以x1=0,x2=
| 3 |
| 2 |
(5)x2-3=0,
△=02-4×1×(-3)=12,
x=
0±
| ||
| 2×1 |
| 3 |
所以x1=
| 3 |
| 3 |
点评:本题考查了解一元二次方程-公式法:把x=
(b2-4ac≥0)叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式.用求根公式解一元二次方程的方法是公式法.
-b±
| ||
| 2a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
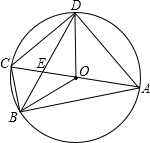 如图,四边形ABCD内接于⊙O,⊙O的直径AC=4,∠BCD=120°,BD与AC的交点为E.
如图,四边形ABCD内接于⊙O,⊙O的直径AC=4,∠BCD=120°,BD与AC的交点为E.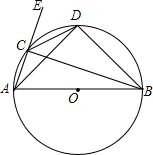 如图,⊙O的直径AB长为6,弦AC长为2,点E在AC的延长线上,∠ECB的平分线交⊙O于点D,求BC和AD的长.
如图,⊙O的直径AB长为6,弦AC长为2,点E在AC的延长线上,∠ECB的平分线交⊙O于点D,求BC和AD的长.