题目内容
 如图,P是⊙O外一点,PA、PC分别与⊙O相交于点A、B和C、D,OF⊥AB,OE⊥CD,已知∠BPO=∠DPO,求证:
如图,P是⊙O外一点,PA、PC分别与⊙O相交于点A、B和C、D,OF⊥AB,OE⊥CD,已知∠BPO=∠DPO,求证: |
| AB |
 |
| CD |
考点:垂径定理,全等三角形的判定与性质,圆心角、弧、弦的关系
专题:证明题
分析:连结OA、OC,如图,根据角平分线定理得到OE=OF,再证明Rt△AOF≌Rt△COE得到AF=CE,然后由垂径定理推知AB=CD,则由圆心角、弧、弦的关系证得结论.
解答: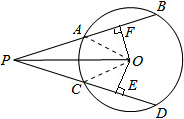 证明:连结OA、OB,如图,
证明:连结OA、OB,如图,
∵∠BPO=∠DPO,即PO平分∠APC,OF⊥AB,OE⊥CD,
∴OF=OE,AF=
AB,CE=
CD,
在Rt△AOF和Rt△COE中,
,
∴Rt△AOF≌Rt△COE,
∴AF=CE,
∴AB=CD,
∴
=
.
 证明:连结OA、OB,如图,
证明:连结OA、OB,如图,∵∠BPO=∠DPO,即PO平分∠APC,OF⊥AB,OE⊥CD,
∴OF=OE,AF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOF和Rt△COE中,
|
∴Rt△AOF≌Rt△COE,
∴AF=CE,
∴AB=CD,
∴
 |
| AB |
 |
| CD |
点评:本题考查了垂径定理:垂直弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了角平分线定理和直角三角形全等的判定方法.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
在⊙O中,弦AB所对的圆心角是40°,弦AB所对的圆周角是( )
| A、20° |
| B、80° |
| C、20°或160° |
| D、80°或100° |
 如图,已知A,B,C,D四个点,请按要求画图:
如图,已知A,B,C,D四个点,请按要求画图: 如图,OC平分∠AOB,∠BOD=2∠AOD.
如图,OC平分∠AOB,∠BOD=2∠AOD. 如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.
如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.