题目内容
如图,双曲线y=| k |
| x |
 过P1和P2向x轴作垂线,垂足为B、D.过P1和P2向y轴作垂线,垂足为A、C.
过P1和P2向x轴作垂线,垂足为B、D.过P1和P2向y轴作垂线,垂足为A、C.(1)若记四边形AP1BO和四边形CP2DO的面积分别为S1和S2,周长为C1和C2,试比较S1和S2,C1和C2的大小;
(2)若P是双曲线y=
| k |
| x |
分析:(1)根据反比例函数中系数k的几何意义可直接得到S1=S2;由于AC、BD的值不能确定,所以应分AC=BD、AC<BD、AC>BD三种情况讨论.
(2)根据题意画出图形,设出P点坐标,根据k为定值,则当x=y时四边形的周长最小.
(2)根据题意画出图形,设出P点坐标,根据k为定值,则当x=y时四边形的周长最小.
解答: 解:(1)根据反比例函数系数k的几何意义可知S1=S2=k;
解:(1)根据反比例函数系数k的几何意义可知S1=S2=k;
当y1-y2=x2-x1,即AC=BD时,C1=C2;
当y1-y2<x2-x1,即AC<BD时,C1<C2;
当y1-y2>x2-x1,即AC>BD时,C1>C2.
(2)设P(x,y),即(x,
),
四边形PMON的周长=2(x+y)=2(x+
),
因为面积相等的四边形中正方形的周长最小,
所以x=
,即x2=k,
解得x=
,
故P点坐标为(
,
).
 解:(1)根据反比例函数系数k的几何意义可知S1=S2=k;
解:(1)根据反比例函数系数k的几何意义可知S1=S2=k;当y1-y2=x2-x1,即AC=BD时,C1=C2;
当y1-y2<x2-x1,即AC<BD时,C1<C2;
当y1-y2>x2-x1,即AC>BD时,C1>C2.
(2)设P(x,y),即(x,
| k |
| x |
四边形PMON的周长=2(x+y)=2(x+
| k |
| x |
因为面积相等的四边形中正方形的周长最小,
所以x=
| k |
| x |
解得x=
| k |
故P点坐标为(
| k |
| k |
点评:本题考查的是反比例函数系数k的几何意义及最值问题,在解(1)时要注意注意分类讨论.

练习册系列答案
相关题目
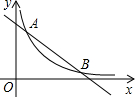 如图,双曲线
如图,双曲线 (2012•扬州)如图,双曲线y=
(2012•扬州)如图,双曲线y=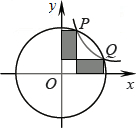 (2012•深圳)如图,双曲线y=
(2012•深圳)如图,双曲线y= 如图,双曲线y=
如图,双曲线y=